
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Тақырып. ҚАТТЫ ДЕНЕ МЕХАНИКАСЫ
|
 материалдық нүктелерінің массаларының олардың қозғалмайтын
материалдық нүктелерінің массаларының олардың қозғалмайтын 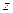 айналу осіне дейінгі арақашықтықтарының
айналу осіне дейінгі арақашықтықтарының
|
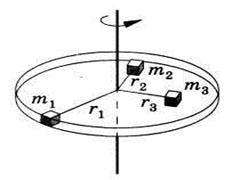
12-сурет
Массаның үздіксіз таралуында бұл қосынды дененің толық көлемі бойынша:  ,
,
мұндағы 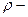 дененің берілген нүктедегі тығыздығы,
дененің берілген нүктедегі тығыздығы, 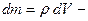 дененің қозғалмайтын айналу осінен
дененің қозғалмайтын айналу осінен  қашықтықта көлемі
қашықтықта көлемі 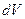 өте кішкентай элементінің массасы. Біртекті дене үшін (
өте кішкентай элементінің массасы. Біртекті дене үшін ( 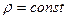 ):
): 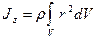 .
.
Штейнер теоремасы:
Дененің кез келген қозғалмайтын айналу осіне қатысты  инерция моменті сол оське параллель массалар центрінен өтетін оське қатысты
инерция моменті сол оське параллель массалар центрінен өтетін оське қатысты 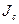 инерция моменті мен дене массасының осы осьтердің арақашықтығының квадратына көбейтіндісінің
инерция моменті мен дене массасының осы осьтердің арақашықтығының квадратына көбейтіндісінің 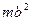 қосындысына тең болады:
қосындысына тең болады:
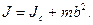 (45)
(45)
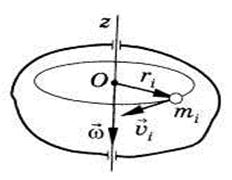
Абсолют қатты дененің өзінің көлемінен өтетін қозғалмайтын  айналу осіне қатысты (13-сурет).
айналу осіне қатысты (13-сурет). 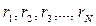 қашықтықта орналасқан массалары
қашықтықта орналасқан массалары
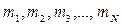 элементар бөліктерден құралған деп ұйға-рылсын. Қатты дене қозғалмайтын
элементар бөліктерден құралған деп ұйға-рылсын. Қатты дене қозғалмайтын  айналу осіне қатысты айналғанда
айналу осіне қатысты айналғанда
|
13-сурет
түрінде өрнектегенде:
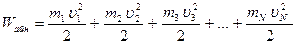 , немесе
, немесе 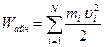 .
.
Cызықтық жылдамдықты бұрыштық жылдамдықпен алмастырғанда,  осі маңында айналатын қатты дененің кинетикалық энергиясы:
осі маңында айналатын қатты дененің кинетикалық энергиясы:
 (47)
(47)
мұндағы 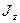 – дененің айналу осіне қатысты инерция моменті.
– дененің айналу осіне қатысты инерция моменті.
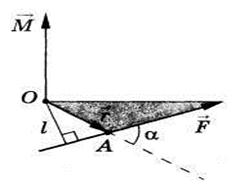
|
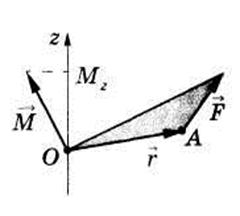 |
14-сурет
15-сурет
|
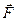 күштің түсу нүктесі (16-сурет).
күштің түсу нүктесі (16-сурет).
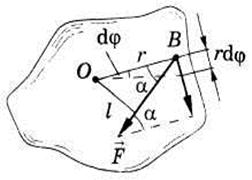
|
16-сурет
Дененің айналу кезіндегі атқарылған жұмыс оның кинетикалық энергиясының артқан шамасына тең болатынын ескерсек,
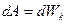 ;
; 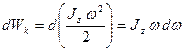 . Осыдан:
. Осыдан: 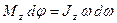 , немесе
, немесе  .
. 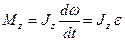 . (50)
. (50)
Осы өрнек қатты дененің қозғалмайтын оське қатысты айналмалы қозғалысының негізгі теңдеуідеп аталады. Айналу z осі дененің масса-лар центрінен өтетін бас инерциялық осьпен дәл келгенде, теңдеу векторлы түрде жазылады:
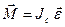 , (51)
, (51)
Қозғалмайтын О нүктеден материалдық нүктеге жүргізілген 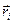 радиус-вектор мен осы материалдық нүктенің
радиус-вектор мен осы материалдық нүктенің  импульсінің векторлық көбей-
импульсінің векторлық көбей-
|
|
тіндісіне тең физикалық шама материалдық нүктенің қозғалмайтын О нүктеге қатысты импульс моменті деп аталады (17-сурет).
 . (52)
. (52)
Импульс моменті векторының модулі: 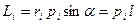 , мұндағы
, мұндағы 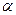 - берілген
- берілген 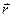 және
және 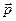 векторларының арасындағы бұрыш,
векторларының арасындағы бұрыш, 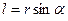 - импульс иіні.
- импульс иіні.
Материалдық нүктенің қозғалмайтын 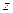 осіне қатысты импульс моменті-берілген осьтің бойындағы кез келген О нүктесіне қатысты анықталған
осіне қатысты импульс моменті-берілген осьтің бойындағы кез келген О нүктесіне қатысты анықталған 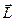 импульс моменті векторының осы оське жүргізілген проекциясына тең скалярлық шама
импульс моменті векторының осы оське жүргізілген проекциясына тең скалярлық шама  (18-сурет).
(18-сурет).
Абсолют қатты дененің қозғалмайтын 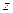 оське қатысты импульс моменті оның жеке бөлшектерінің сол оське қатысты импульс моменттерінің қосындысына тең:
оське қатысты импульс моменті оның жеке бөлшектерінің сол оське қатысты импульс моменттерінің қосындысына тең:

 . (53)
. (53)
Сызықтық жылдамдықты бұрыштық жылдамдықпен алмастырғанда:
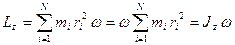 .
.
Теңдеуді уақыт бойынша дифференциалдағанда:
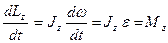 , немесе:
, немесе: 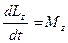 . (54)
. (54)
Осы формула - қатты дененің қозғалмайтын 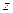 оське қатысты айналмалы қозғалысы теңдеуініңтағы бір түрі: қатты дененің қозғалмайтын
оське қатысты айналмалы қозғалысы теңдеуініңтағы бір түрі: қатты дененің қозғалмайтын 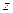 айналу осіне қатысты импульс моментінің уақытпен алынған туындысы осы оське қатысты күш моментіне тең.
айналу осіне қатысты импульс моментінің уақытпен алынған туындысы осы оське қатысты күш моментіне тең.
Егер z айналу осі дененің массалар центрінен өтетін бас инерциялық осьпен дәл келсе, теңдеу векторлы түрге көшеді:
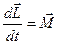 . (55)
. (55)
Тұйық жүйеде сыртқы күштердің моменті  және
және 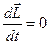 . Осыдан:
. Осыдан:
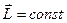 , (56)
, (56)
яғни, механикалық тұйық жүйенің импульс моменті тұрақты болады(импульс моментінің сақталу заңы).
Бұл заң кеңістіктің симметриялық қасиеті – изотроптылықпен байланысты.
Дата добавления: 2014-10-31; просмотров: 649; Мы поможем в написании вашей работы!; Нарушение авторских прав |
 .
Инерция моменті – аддитивтік шама: қатты дененің инерция моменті оның құрамдас бөліктерінің инерция моменттерінің қосындысына тең.
.
Инерция моменті – аддитивтік шама: қатты дененің инерция моменті оның құрамдас бөліктерінің инерция моменттерінің қосындысына тең.
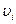 сызықты жылдамдықпен радиустары
сызықты жылдамдықпен радиустары 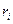 шеңберлер сызады. Олардың бұрыштық жылдамдықтары бірдей болатынын
ескеріп:
шеңберлер сызады. Олардың бұрыштық жылдамдықтары бірдей болатынын
ескеріп:  , (46)
дененің кинетикалық энергиясын масса-лары
, (46)
дененің кинетикалық энергиясын масса-лары  бөліктерінің кине-
тикалық энергияларының қосындысы
бөліктерінің кине-
тикалық энергияларының қосындысы
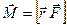 (48)
Күш моменті векторының модулі
(48)
Күш моменті векторының модулі
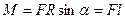 , мұндағы
, мұндағы 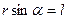 -күш иіні. Күш моментінің векторы
-күш иіні. Күш моментінің векторы 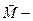 сағат тілініңбағытыменбұранданың
сағат тілініңбағытыменбұранданың 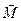 күш моменті векторының осы оське жүргі-зілген проекциясына тең скалярлық шама (15-сурет).
күш моменті векторының осы оське жүргі-зілген проекциясына тең скалярлық шама (15-сурет).
 бұрышқа бұрыл-ғанда В нүктесі
бұрышқа бұрыл-ғанда В нүктесі  жол өтіп, орындалған жұмыс күштің ығысу бағытына проекциясын
жол өтіп, орындалған жұмыс күштің ығысу бағытына проекциясын 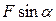 ығысу шамасына
ығысу шамасына 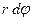 көбейткенге тең:
көбейткенге тең: 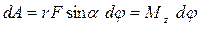 . (49)
. (49)
