
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Д і с т е о р и я с ы. Тербеліс - белгілі бір уақыт аралығында қайталанып отыратын қозғалыс немесе процесс
Тербеліс - белгілі бір уақыт аралығында қайталанып отыратын қозғалыс немесе процесс. Тербелмелі жүйенің бастапқы берілген энергия есебінен сыртқы күштердің әсерінсіз тербелісі еркін (немесе меншікті) тербеліс деп аталады. Егер тербелмелі жүйе бірдей уақытта тепе-теңдік жағдайына келіп отырса, тербеліс периодты деп аталады. Қарапайым периодты тербе-лістерге дененің немесе жүйенің тепе-теңдік қалпынан ығысуы синус немесе косинус заңымен сипатталатын гармоникалық тербелістер жатады.
Серпімді Fсер= -kx күштің әсерінен гармоникалық тербеліс жасайтын серіппеге ілінген массасы m жүк серіппелі маятник деп аталады (1-сурет).
Серіппелі маятниктің тербелісін қарастыру бары-









 сында келесі жағдайларды ескеру қажет:
сында келесі жағдайларды ескеру қажет:
 - ортаның кедергісін ескерілмейді;
- ортаның кедергісін ескерілмейді;

 - тепе-теңдік жағдайда маятникке шамалары бір-
- тепе-теңдік жағдайда маятникке шамалары бір-
 біріне тең, бағыттары қарсы серпімділік және
біріне тең, бағыттары қарсы серпімділік және
 ауырлық күші әсер етеді;
ауырлық күші әсер етеді; 


 - маятникті төмен тартқанда тепе-теңдікке қарай
- маятникті төмен тартқанда тепе-теңдікке қарай

 m бағытталған қосымша серпімділік күш болады.
m бағытталған қосымша серпімділік күш болады.
0 2х Маятник жоғары орынға келгенде осындай 

 жағдай қайталанады, бірақ күштің табиғаты бас-
жағдай қайталанады, бірақ күштің табиғаты бас-

 х қаша: ауырлық және серпімділік күштерінің тең
х қаша: ауырлық және серпімділік күштерінің тең
әсерлі күші шамасы жағынан маятниктің
1-сурет тепе-теңдіктен x ығысу шамасына пропорционал.
Тепе-теңдік қалпынан ауытқыған маятникке әсер ететін кері қайтарушы квазисерпімді күш Гук заңы бойынша:
Fсер = -k x, (1)
Сонда Ньютонның 2-заңы бойынша
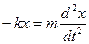 (2)
(2)
мұндағы мұндағы k - серіппенің серпімділік коэффициенті (қатаңдығы),
m -маятниктің массасы, a=  - ауытқудың уақыт бойынша алынған екінші ретті туындысымен анықталатын тербеліс үдеуі. (2) теңдеуді түрлендіріп,
- ауытқудың уақыт бойынша алынған екінші ретті туындысымен анықталатын тербеліс үдеуі. (2) теңдеуді түрлендіріп,  w02 алмастырғанда, еркін гармоникалық тербелістің дифференциалдық теңдеуі (динамикалық теңдеу) шығады:
w02 алмастырғанда, еркін гармоникалық тербелістің дифференциалдық теңдеуі (динамикалық теңдеу) шығады:
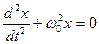 (3)
(3)
Бұл дифференциалдық теңдеудің шешімі мына функциямен өрнектеледі:
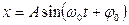 немесе
немесе  (4)
(4)
Осы формула бойынша серіппелі маятниктің кез келген уақыт мезетіндегі тепе-теңдіктен ауытқу мәні анықталады (гармоникалық тербелістің жалпы түрдегі кинематикалық теңдеуі). Мұндағы:
А - амплитуда, яғни тепе-теңдіктен ауытқудың максимал шамасы;
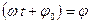 – фаза, тербелмелі жүйенің кез келген t уақыт мезетіндегі орнын анықтайтын шама;
– фаза, тербелмелі жүйенің кез келген t уақыт мезетіндегі орнын анықтайтын шама;
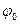 – тербелістің бастапқы фазасы, яғни бастапқы t =0 уақыт мезетіндегі тербелмелі жүйенің орнын анықтайтын шама;
– тербелістің бастапқы фазасы, яғни бастапқы t =0 уақыт мезетіндегі тербелмелі жүйенің орнын анықтайтын шама;
 – гармониялық тербелістің бұрыштық (циклдік) жиілігі, яғни 2p секунд уақыт ішіндегі толық тербеліс саны.
– гармониялық тербелістің бұрыштық (циклдік) жиілігі, яғни 2p секунд уақыт ішіндегі толық тербеліс саны.
Толық бір тербеліс орындалатын уақыт - период (Т), бірлік уақыт ішінде жасалатын тербелістер саны тербеліс жиілігі (n) деп аталады. Тербеліс жиілігі n, бұрыштық жиілік 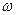 және тербеліс периоды Т өзара байланысты:
және тербеліс периоды Т өзара байланысты:
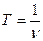 ;
;  ;
;  ;
;
 болатынын ескерсек, серіппелі маятниктің периоды:
болатынын ескерсек, серіппелі маятниктің периоды:
 . (5)
. (5)
Серпімділік коэффициентінің k физикалық мағынасын ашайық:
 , (6)
, (6)
Мұндағы Fд –деформация күші, Ньютонның 3-заңына сәйкес Fд= -Fс. Осыдан, серпімділік коэффициенті k - серіппені бірлік ұзындыққа деформациялайтын сыртқы күшке сан жағынан тең шама.
Нақты тербелмелі жүйеде уақыт өтуіне қарай энергия жоғалуы салдарынан амплитудасы кемитін тербеліс өшетін тербеліс деп аталады. Мұндай тербелістер үйкеліс 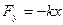 күші мен кедергі күшінің
күші мен кедергі күшінің 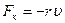 бір мезгілде әсер етуінен болады, мұндағы
бір мезгілде әсер етуінен болады, мұндағы 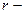 ортаның кедергі коэффициенті,
ортаның кедергі коэффициенті,  тербеліс жылдамдығы. Өшетін тербелістің дифференциалдық теңдеуі:
тербеліс жылдамдығы. Өшетін тербелістің дифференциалдық теңдеуі:
 . (7)
. (7)
Теңдеудің шешімі өшетін тербелістің кинематикалық теңдеуі болады:
 . (8)
. (8)
Мұнда A0 -бастапқы амплитуда ( t=0); e- натурал логарифмнің негізі;
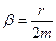 - тербелістің өшу коэффициенті;
- тербелістің өшу коэффициенті; 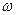 - еркін өшетін тербелістің циклдік жиілігі. Өшетін және өшпейтін тербелістердің циклдік жиіліктері арасындағы байланыс:
- еркін өшетін тербелістің циклдік жиілігі. Өшетін және өшпейтін тербелістердің циклдік жиіліктері арасындағы байланыс:  .
.
Еркін өшетін тербелістердің амплитудасы уақыт өтуіне қарай экспоненциалдық заңдылықпен кемиді:
 (9)
(9)
Тербелмелі қозғалыстың өшу жылдамдығы уақыт аралығы бір период көршілес екі тербелістің амплитудаларының қатынасына тең шама - өшу декрементімен сипатталады (2-сурет):
 (10)
(10)
Өрнектің натурал логарифмі өшудің логарифмдік декременті деп аталады:
 (11)
(11)
Өшетін тербелістердің периодын анықтай отырып, өшу коэффициентін  және өшудің логарифмдік декрементін
және өшудің логарифмдік декрементін 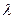 есептеуге болады.
есептеуге болады.
 x
x
A0 A1 An+T
t
T
nT
2-сурет
Ол үшін бір-бірінен уақыт бойынша бір периодқа кешігіп отыратын екі амплитуда өлшенеді, яғни t= nT уақыт үшін:
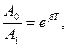

 ... ,
... , 
қатынастары бойынша:  (12)
(12)
Демек:  (13)
(13)
Осыдан өшу коэффициенті: 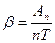 (14)
(14)
Дата добавления: 2014-10-31; просмотров: 1565; Мы поможем в написании вашей работы!; Нарушение авторских прав |