МАКСВЕЛЛ ТЕОРИЯСЫ

Максвелл теориясы–электр зарядтары мен токтардың кез келген жүйесінің электрмагниттік өрісі туралы бірегей теория. Бұл теорияда электрдинамиканың негізгі сұрақтары шешілген: зарядтар мен токтардың таралуы арқылы олардың электр және магнит өрістерінің сипаттамалары тұжырымдалады.

Максвелл теориясы электрмагниттік құбылыстарды суреттейтін маңызды заңдардың: Остроградский–Гаусс теоремасының, толық ток заңының, электрмагниттік индукция заңының жинақты қорытындысы болып есептеледі.

Максвелл теориясы–макроскопиялық, мұнда кеңістіктік таралуы атомдар мен молекулалар өлшемінен көп ретті есе салыстырмалы тыныштықтағы және қозғалыстағы зарядтар жүйесінің макроскопиялық электрмагниттік өрістері зерттелген.

Максвелл теориясы–жақыннан әрекеттесу теориясы: электрлік және магниттік өзара әрекеттесулер электрмагниттік өріс арқылы орындалады және берілген ортадағы жарық жылдамдығына тең шекті жылдамдықпен таралады.

Максвелл теориясының негізіне төрт теңдеу алынған.

Максвелдің интегралдық түрдегі бірінші теңдеуі Фарадейдің электрмагниттік индукция заңын қорытындылау болып есептеледі. Максвелл бойынша, уақыт өтуімен өзгеріп тұратын магнит өрісі циркуляциясы электрмагниттік индукцияның ЭҚК тең құйынды электр өрісін тудырады:

. (155)

Яғни, тек электрлік зарядтар ғана емес, уақыт бойынша өзгеретін айнымалы магнит өрісі де электр өрісінің көзі бола алады. Векторлық анализдегі Стокс теоремасын қолданып:

=Қандай да бір S беттің әрбір нүктесінде векторының роторын біле отырып, осы бетті шектейтін L контурының бойымен векторының циркуляциясын есептеп:

.

дифференциалдық түріне көшуге болады:

(156)

Максвелдің интегралдық түрдегі екінші теңдеуі толық ток заңына негізделген. Максвелл бойынша, уақыт өтуімен айнымалы электр өрісі қоршаған ортада құйынды магнит өрісін туғызады. Айнымалы электр өрісінің магниттік ықпалының сандық өлшемі – ығысу тогы – қоршаған ортада (вакуумде немесе затта) магнит өрісін қоздыруға қабілетті. Айнымалы ток тізбегінде толық ток әрқашан тұйықталған, яғни сымның шеттерінде тек өткізгіштік тогы ғана үзіледі, ал диэлектрикте (вакуумде) сымның ұштарында өткізгіштік токтарын тұйықтайтын ығысу тогы бар болады. Сәйкесінше, толық токтың тығыздығы:

.

Мұндағы толық токтың тығыздығы, – өткізгіштік тогының тығыздығы, 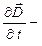ығысу тогының тығыздығы. Осыдан толық ток:

.

векторының циркуляциясы туралы теореманы қорытындылай келе, Максвелдің интегралдық түрдегі екінші теңдеуі шығады:

. (157)

Яғни, қозғалыстағы электрлік зарядтар (электр тогы)немесе айнымалы электр өрісі магнит өрісінің көзі бола алады. Векторлық анализдегі Стокс теоремасын қолданып дифференциалдық түріне көшуге болады:

. (158)

Максвелдің интегралдық түрдегі үшінші теңдеуі– электрстатикалық өріске арналған Остроградский –Гаусс теоремасы айнымалы электр өрісі үшін де орындалады деп қорытындылайды:

.

Заряд тұйық беттің ішінде көлемдік тығыздықпен үзіліссіз таралса:

(159)

Векторлық анализдегі Гаусс теоремасын қолдану арқылы:

=Кеңістіктің әрбір нүктесіндегі векторының дивергенциясын біле отырып, осы вектордың кез келген шекті өлшемді тұйық S бетті қиып өтетін ағынын есептеуге болады:

,

үшінші теңдеудің дифференциалдық түрі былай жазылады:

. (160)

Максвелдің интегралдық түрдегі төртінші теңдеуі кез келген магнит өрісі үшін Остроградский –Гаусс теоремасы орындалады деп қорытындылайды:

. (161)

Векторлық анализдегі Гаусс теоремасына сәйкес төртінші теңдеу дифференциалдық түрде былай жазылады:

. (162)

Тұрақты электр және магнит өрістері бір-бірінен тәуелсіз болады. Электр өрісі электрстатиканың екі теңдеуімен сипатталады:

немесе ,

немесе .

Магнит өрісі магнитстатиканың екі теңдеуімен сипатталады:

немесе ,

немесе .

Зарядтар мен токтар кеңістікте үзіліссіз таралса, Максвелл теңдеулерінің интегралдық және дифференциалдық түрлері пара-пар болады. Кеңістікте нақты ортаның немесе өрістің қасиеті кенеттен секірмелі түрде өзгеретін үзілісті беттерде интегралдық түрдегі теңдеулер қолдануға ыңғайлы.