Статически неопределимые системы

Системы, внутренние силы в элементах которых невозможно определить при помощи лишь одних уравнений статики, называются статически неопределимыми. Такие системы имеют «лишние» связи: внешние (опорные) или внутренние. Будем рассматривать только внешние ста­тически неопределимые системы.

Степень статической неопределимости определяется разностью между числом неизвестных реакций (связей) и числом независимых уравнений статики. Для раскрытия статической неопределимости к уравнениям статики нужно составить столько дополнительных уравнений, сколько раз статически неопределима система. Эти дополнитель­ные уравнения составляются из условий совместности деформаций.

Существуют несколько методов раскрытия статической неопределимости. Наиболее простой – метод сравнения перемещений (деформа­ций). Суть этого метода заключается в сравнении перемещений (деформаций) от заданной нагрузки и от реакции опоры в одностержневых системах и сопоставлении деформаций стержней в многостержневых системах. Раскрытие статической неопределимости для одиночных стержней, работающих на растяжение-сжатие, кручение и изгиб, однотипно. Для ведения расчета выбирается основная система, которая получается из заданной путем удаления лишних связей и, следовательно, является статически определимой (основная система, загруженная внешними силами и неизвестной реакцией, соответствующей удаленной связи, называется эквивалентной системой). Затем составляется дополнитель­ное уравнение, которое характеризует перемещение (деформацию) в сечении, где удалена связь.

Пример 2

Раскрыть статическую неопределимость ступенчатого стержня, изготовленного из стали Ст3 (рис. 6, а) и построить эпюру продольных сил. Модуль упру­гости материала стержня Е равен 200 ГПа (прил. 3).

Стержень имеет две неизвестные опорные реакции С и В (направляем произвольно). Уравнение статики можно составить только одно:

ΣY =С + F₂ – F₁ + В = 0.

Таким образом, система один раз статически неопределима. Основную систему получим, удалив связь, принадлежащую, например, опоре В. Эквивалентная система показана на рис. 6, б.

В сечении В заданной системы перемещение равно нулю. Значит, и в эквивалентной системе должно выполняться это условие δ_В = 0. Это и есть дополнительное уравнение. Для раскрытия его используем принцип независимости действия сил. Перемещение сечения В равно алгебраической сумме деформации всех участков стержня, вычисленных от каждой силы в отдельности.

Рассматривая эквивалентную систему, заметим, что реакция В сжимает все участки стержня, сила F₁ растягивает участки II, III и IV_, а сила F₂ сжимает участок IV.

_B

откуда В = 61·10³ Н = 61кН (направление совпадает с выбранным).

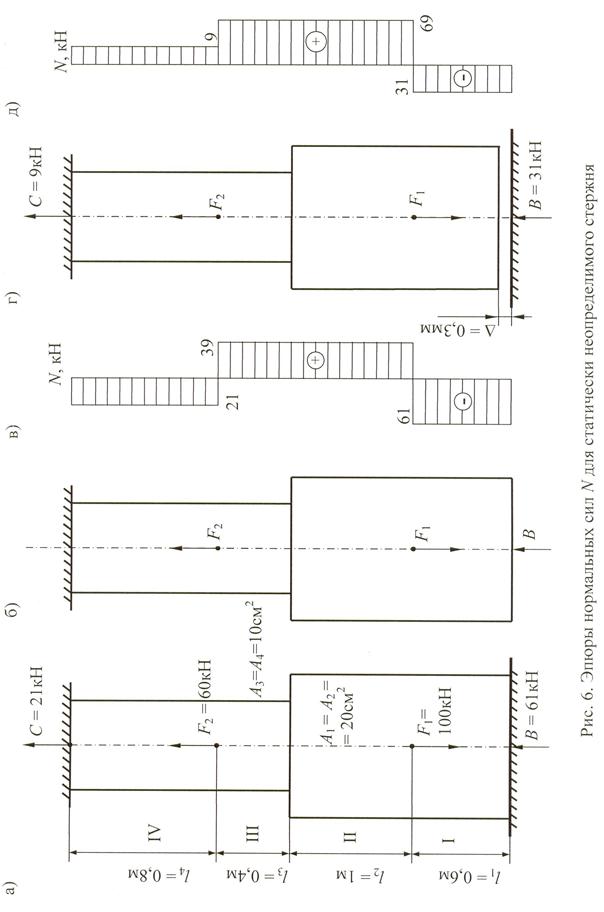
Опорную реакцию С определим из уравнения статики:

С + 60 – 100 + 61 = 0,

откуда С = – 21 кН (направление обратное).

Эпюра продольных сил N, построенная обычным образом (см. прим. 1), показана на рис. 6, в.

Опорную реакцию С можно определить аналогично реакции В, а уравнение статики – использовать для проверки правильности вычислений. Проделайте это самостоятельно.

Если рассматриваемый стержень вследствие неточности изготовления не будет достигать опоры на величину Δ (рис. 6, г), то дополнительное уравнение приметвид δ_В = Δ.Нарис. 6,дпоказана эпюра N при Δ=0,03см.