
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Расчет на прочность
Плоским (прямым) поперечным изгибом балки называется изгиб, при котором все внешние нагрузки действуют в одной из главных плоскостей инерции балки, причем проекции внешних сил и реакций опор на ось балки равны нулю. В этом случае отличны от нуля только две из шести внутренних сил: внутренняя поперечная сила Qy и внутренний изгибающий момент Mz., действующий в этой же плоскости, где приложены внешние силы (рис. 23).
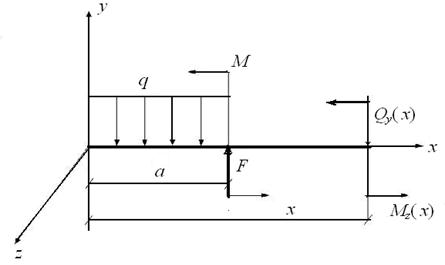
Рис. 23. Внутренние силы в поперечном сечении балки:
поперечная сила Qy(х) и изгибающий момент Mz.(х)
Эти внутренние силы определяются методом сечений из условий статического равновесия части балки, расположенной по одну сторону от рассматриваемого сечения, под действием внешней нагрузки и искомых внутренних сил, действующих со стороны отброшенной части балки. Условия статического равновесия сводятся к двум уравнениям статики: равенстве нулю суммы проекций на ось у всех сил (ΣY = 0) и равенстве нулю суммы моментов в сечении х всех сил (Σmx = 0).
Для балки (см. рис 23) поперечная сила Qy(х) и изгибающий момент Mz.(х) определяются из двух уравнений статического равновесия:
ΣY = F – q∙a –- Qy(х) = 0,

откуда
Qy(х) = F – q∙a, (2)
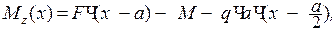 (3)
(3)
При выполнении условий (2) и (3) все остальные условия статического равновесия удовлетворяются автоматически, т. е. никаких других внутренних сил при плоском изгибе не возникнет.
Из (2) и (3) видим, что внутренняя поперечная сила Qy(х) в сечении x численно равна алгебраической сумме всех внешних сил, действующих по одну сторону от рассматриваемого сечения. Аналогично, внутренний изгибающий момент Mz(х) в сечении х численно равен алгебраической сумме моментов всех внешних нагрузок, действующих по одну сторону от рассматриваемого сечения.
Для того, чтобы внутренние силы определялись однозначно и независимо от того, равновесие какой части балки рассматривается, вводят правило знаков для Qy(х) и Mz(х).
Если внешняя сила (F, q) стремится повернуть рассматриваемую часть балки относительно центра тяжести сечения x по ходу часовой стрелки, то ее вклад во внутреннюю силу Qy(х) положителен, если против хода часовой стрелки – отрицателен (рис. 24).

Рис. 24. Определение знака поперечной силы Qy(х)
Если внешняя сила (F, q, M) стремится изогнуть часть балки относительно центра тяжести сечения х выпуклостью вниз (сжатое волокно сверху), то ее вклад во внутренний момент Mz(х) положителен; если выпуклостью вверх (сжатое волокно снизу) – отрицателен (рис. 25).
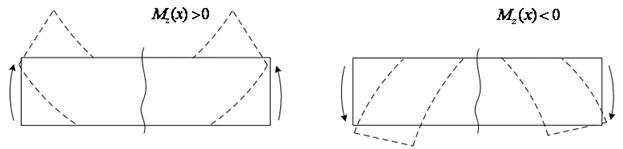
Рис. 25. Определение знака изгибающего момента Mz(х)
Направим ось абсцисс (ox) системы координат слева направо вдоль оси балки. Тогда внутренние усилия Qy(х), Mz(х) в поперечных сечениях и внешняя распределенная нагрузка q будут функциями x. Они связаны дифференциальными соотношениями:
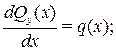 (4)
(4)
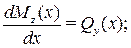 (5)
(5)
 (6)
(6)
Здесь q(х) считается положительной, если она направлена вверх. Эти соотношения следует использовать при проверке правильности построения эпюр Qy(х) и Mz(х).
Внутренний изгибающий момент связан с нормальными напряжениями, которые распределяются по высоте сечения неравномерно, вызывая растяжение одной его части и сжатие другой.
Условие прочности по нормальным напряжениям для балки любой формы поперечного сечения имеет вид
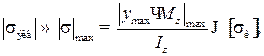 (7)
(7)
где Mz – изгибающий момент в опасном сечении балки, Н∙м;
Iz – момент инерции поперечного сечения, м4;
ymax – расстояние от нейтральной оси до наиболее удаленной точки
поперечного сечения, м.
Для балок, поперечные сечения которых симметричны относительно нейтральной оси z, условие прочности преобразуется к виду
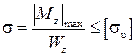 , (8)
, (8)
где Wz – осевой момент сопротивления поперечного сечения, м3.
На основании соотношений (7), (8) Wz определяется по формуле

Поперечная сила Qy(х), вектор которой лежит в плоскости поперечного сечения, вызывает в точках сечения касательные напряжения τxy. По закону парности касательных напряжений на продольных площадках возникают равные им напряжения τyх = τxy = τ...
Напряжения τxy возникают вследствие деформации среза поперек продольных волокон балки, а напряжения τyх вызваны деформацией сдвига продольных волокон вдоль балки.
Для балок постоянного поперечного сечения при допущении, что касательные напряжения τ. по ширине сечения b распределены равномерно, касательные напряжения при изгибе определяются по формуле Журавского:
 ,
,
где  – статический момент относительно оси z отсеченной части сечения;
– статический момент относительно оси z отсеченной части сечения;
b – ширина сечения;
Iz – осевой момент инерции сечения.
Интенсивность сдвигающих усилий Т (погонная сдвигающая сила) определяется равенством
 .
.
Касательные напряжения распределяются по сечению неравномерно, достигая максимального значения на нейтральной оси. Как показывают расчеты, в балках, поперечные размеры которых много меньше их длины, касательные напряжения в поперечных сечениях значительно меньше нормальных, поэтому, если балка изготовлена из изотропного материала, то при записи условия прочности касательные напряжения можно не учитывать, именно поэтому σэкв ≈ σ.
6.1.1. Построение эпюр внутренних сил Qy и Mz
Эпюрой внутренней силы называется график ее изменения вдоль оси балки. Из определения внутренней поперечной силы Qy(х) следует, что в том и только в том сечении, где приложена внешняя сосредоточенная сила, имеется скачок на эпюре Qy(х) на величину этой силы. Аналогично из определения внутреннего изгибающего момента Mz(х) следует, что в том и только в том сечении, где приложен внешний изгибающий момент, – скачок на эпюре Mz(х) на величину этого момента. Под внешними силами и моментами мы подразумеваем и реакции опор.
При проверке правильности построения эпюр Qy(х) и Mz(х) можно использовать табл. 6, составленную на основании дифференциальных соотношений (4) – (6). В этой таблице указана связь между знаками интенсивности распределенной нагрузки q(x), поперечной силы Qy(х) и характером изменения эпюр Qy(х) и Mz(х) .
Таблица 6
Правила построения эпюр Qy(х) и Mz(х) , основанные
на дифференциальных зависимостях между q, Qy(х), Mz(х)
| Распреде-ленная нагрузка q, кН/м | Поперечная сила Qy, кН | Изгибающий момент Mz, кН∙м |
| q=0 | Поперечная сила постоянна | Изгибающий момент изменяется по линейному закону |
| Момент постоянный ______ | ||
| + |  Момент возрастает Момент возрастает
| |
| _ |  Момент убывает Момент убывает
| |
| q >0 | Поперечная сила возрастает по линейному закону | Момент изменяется по закону параболы, выпуклость вниз |
| Момент принимает экстремальное значение Mmin | ||
| + | Момент возрастает по закону параболы, выпуклость вниз

| |
| _ | Момент убывает по закону параболы, выпуклость вниз

| |
| q < 0 | Поперечная сила убывает по линейному закону | Момент изменяется по закону параболы, выпуклость вверх |
| Момент принимает экстремальное значение Mmax | ||
| + | Момент возрастает по закону параболы, выпуклость вверх
| |
| _ | Момент убывает по закону параболы, выпуклость вверх
|
Дата добавления: 2014-11-13; просмотров: 335; Мы поможем в написании вашей работы!; Нарушение авторских прав |