Пример 6

Рассмотрим построение эпюр Q_y(х) и M_z.(х) методом записи и исследования их уравнений на примере расчета на прочность двухопорной балки.

Необходимо построить эпюры поперечных сил Q_y и изгибающих моментов M_z для двухопорной двутавровой балки (рис. 26) и подобрать размеры поперечного сечения при 200 МПа.

1. Определение опорных реакций:

;

;

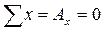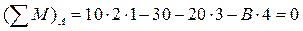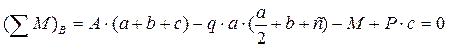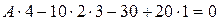, кН;

;

, кН.

Проверка следова-тельно, реакции найдены верно.

2. Построение эпюр Q_y и M_z.

Балка имеет три участка нагружения.

Участок I

В пределах первого участка произвольно намечаем сечение

(см. рис. 26): м.

Для составления уравнений Q_y(х₁) и M_z(х₁) рассмотрим условия равновесия левой (от сечения ) части балки. Поперечная сила в сечении равна алгебраической сумме внешних сил по левую сторону от сечения.

Учитывая правило знаков (см. рис. 24), получим Q_y(х) = A – q∙x₁ = = 17,5 – 10∙x₁ (кН) – линейная зависимость.

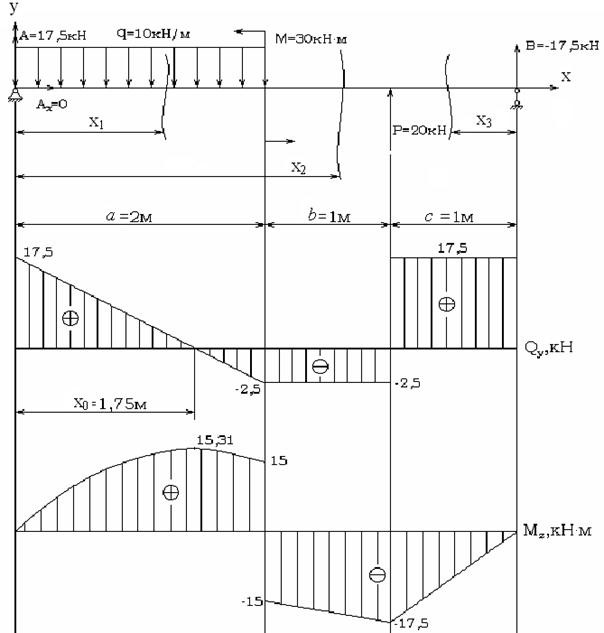
Рис. 26. Построение эпюр Q_y(x) и M_z(x) для двухопорной балки

График поперечной силы Q_y(х) можно построить по двум точкам, абсциссы которых соответствуют границам участка I:

Q_y(0) = 17,5 кН; Q_y(2) = – 2,5 кН.

Далее нам нужно найти точку пересечения эпюры с базисной линией, т. е.

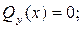
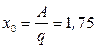. (9)

Внутренний изгибающий момент в сечении равен алгебраической сумме моментов от всех внешних нагрузок по левую сторону от сечения. С учетом правила знаков (см. рис. 25) получим

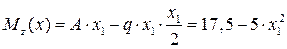– парабола ветвями вниз. Значения на границах участка 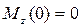, 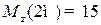кН∙м.

Вершина параболы находится из условия

,

т. е. из (9) при м кН∙м.

По трем точкам строим эпюру M_z на участке I.

Участок II

Наметив сечение , рассмотрим левую часть балки:

м,

Q_y( x₂) = A – q∙2 = 17,5 – 20 = – 2,5 кН – (10)

– горизонтальная прямая, тaк как Q_y( x₂) = – 2,5 кН – const.

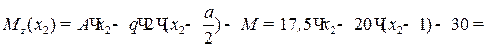(11)

= – 2,5∙х₂ – 10 кН∙м –

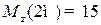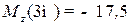– прямая линия. кН∙м, кН∙м.

Можно убедиться, что из условия равновесия правой части балки

получаются те же самые выражения (10) и (11) для внутренних сил:

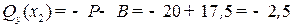кН;

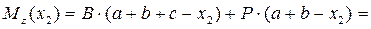
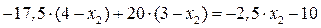кН∙м.

Участок III

Здесь проще рассматривать условие равновесия правой части балки

м.

Учитывая правила знаков для правой части балки (см. рис. 24, 25), получим:

– горизонтальная прямая.

,

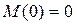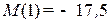, кН∙м.

Построив эпюры 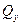и 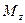(см. рис. 26), проверяем, удовлетворяют ли

они правилам, сформулированным в табл. 6.

3. Расчет на прочность.

Условие прочности при прямом изгибе можно приближенно

записать в виде неравенства

,

откуда находим момент сопротивления поперечного сечения.

Вычисления производим в системе СИ:

.

По сортаменту (см. прил. 5) определим, что такому условию соответствует двутавр № 16, W_z = 109 см³.

6.1.2. Построение эпюр внутренних сил Q_y и M_z