Без записи их уравнений

Изучив закономерность изменения Q_y и M_z на участках балки в зависимости от характера нагрузки, эпюры можно строить не по их уравнениям, а по отдельным ординатам, вычисленным для характерных сечений. Характерными являются сечения границ участков балки, а также сечения, где Q_y меняет знак.

В отличие от способа построения эпюр, рассмотренного выше, где качественные особенности эпюр (интервалы возрастания и убывания, точки экстремумов и разрывов) выявляются только в результате их построения, а затем проверяются в соответствии с табл. 6, в данной методике эти качественные особенности используются непосредственно для построения эпюр. Как показывает практика, при этом не только уменьшается объем вычислений, но и снижается вероятность ошибки.

Рассмотрим этот метод на примере балки, представленной на рис. 26.

1. Построение эпюры Q_y

Рисуем график эпюры в виде непрерывной линии так, что абсцисса x возрастает (идем слева направо). При этом в соответствии с правилом знаков для Q_y, встретив положительную по алгебраической величине сосредоточенную силу, направленную вверх, делаем на эпюре Q_y скачок вверх на величину этой силы (если сила направлена вверх, но ее значение отрицательно, то скачок вниз). Встретив силу, положительную по алгебраической величине, направленную вниз, делаем скачок вниз. Так как 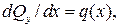то из физического смысла производной q – скорость роста функции Q_y. Если на участке 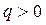(направлена вверх), то эпюра 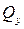растет при увеличении x. Если 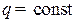, то 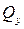изображается прямой линией. Чтобы найти величину возрастания эпюры Q_y на участке, нужно q умножить на длину этого участка. Соответственно, если 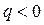(направлена вниз), то 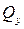убывает; если 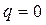, то

Для иллюстрации построения эпюр без записи их уравнений рассмотрим расчетную схему, приведенную на рис. 26.

Участок I

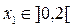м,

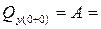17,5 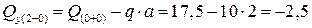кН,

кН.

Точка, где поперечная сила Q_y(x) равна нулю,

,

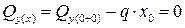отсюда 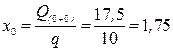м.

Так как 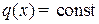, то график 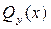– прямая линия.

Участок II

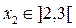м,

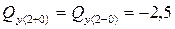кН (скачка нет),

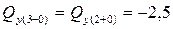кН.

График функции 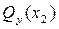– горизонтальная прямая.

Участок III

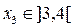м,

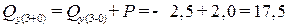кН – скачок вверх на величину силы P; 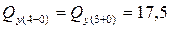кН.

График функции 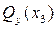– горизонтальная прямая.

Можно считать, что балка продолжается и правее сечения x = 4 м.

Тогда все внутренние силы в сечениях x > 4 м должны быть равны нулю (из условия равновесия правой части). Проверим это:

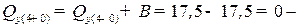
– скачок вниз на величину силы B – проверка сошлась.

2. Построение эпюры M_z

График эпюры M_z также будем строить в порядке возрастания абсциссы x (идем слева направо). Скачки на эпюре M_z наблюдаются в тех и только в тех точках, где приложены сосредоточенные моменты сил, причем если положительный по алгебраической величине момент направлен по часовой стрелке, то в соответствии с правилом знаков (см. рис. 24, где рассматривается равновесие левой части), имеется скачок вверх на величину внешнего момента. Если встретили внешний момент, вращающий против часовой стрелки, – рисуем скачок вниз.

Так как 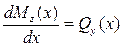, то Q_y(x) – скорость роста функции M_z(x). Если на участке 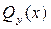>0, то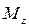 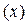растет, при 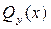= 0

M_z(x) = const; если 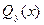< 0, M_z(x) убывает с ростом аргумента x. В том сечении внутри участка, где Q_y(x) меняет знак, на эпюре M_z(x) – экстремум. Если внутри участка Q_y(x) = const, то M_z(x) – прямая; если же 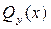– наклонная прямая, то эпюра M_z(x) изображается параболой. Иначе говоря, на тех участках, где распределенная нагрузка отсутствует 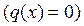эпюра M_z(x) изображается прямой линией, а там, где 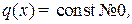M_z(x) изображается параболой. Направление выпуклости параболы – навстречу распределенной нагрузке (рис. 27).

Для того, чтобы найти величину изменения внутреннего момента M_z на заданном участке, нужно среднее значение скорости изменения момента 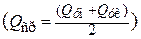умножить на длину участка. Иными словами, величина изменения внутреннего изгибающего момента M_z на участке равна площади эпюры Q_y на этом участке:

M_zк‏‏ = M_zн + Q_ср‏‏ ∙ L, (12)

где M_zк‏‏ – значение внутреннего момента в конце, а M_zн – в начале участка длиной L;

Q_ср – среднее значение внутренней поперечной силы на этом участке.

Формула (12) справедлива для любого участка, внутри которого нет внешних изгибающих моментов.

Участок I

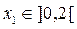м.

Так как в начале участка нет сосредоточенного момента, то .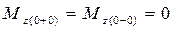

Значение момента в точке максимума (x = 1,75 м) и в конце участка вычисляем по формуле (12):

;

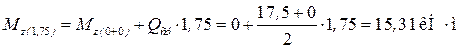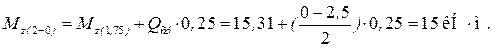
Можно сделать проверку:

.

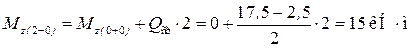Строим параболу выпуклостью вверх.

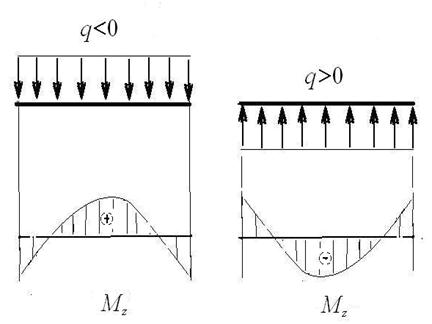
Рис. 27. Направление выпуклости параболы M_z

в зависимости от знака распределенной нагрузки q

Участок II

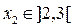м.

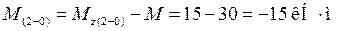– на границе I и II участков скачок вниз на величину момента М.

Значение изгибающего момента в конце участка II:

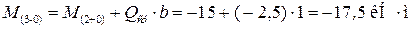
Так Q_y на этом участке постоянна и отрицательна, то эпюра M_z изображается прямой линией и убывает. Строим эту прямую по двум точкам.

Участок III

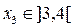м.

Так как в сечении x = 3 м нет внешнего момента, то

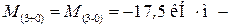скачка нет.

Так как Q_y положительна и постоянна, то на эпюре M_z – рост по

прямой.

,

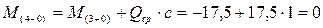как и должно быть из условия равновесия правой части (проверка сошлась).

 

Задача 6. Плоский изгиб (консольная балка)

Произвести расчет на прочность консольной балки. Схемы балок представлены на рис. 28, данные к задаче приведены в табл. 7. Материал балки – сталь с 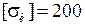МПа.

План решения задачи:

1) построить эпюры поперечных сил и изгибающих моментов;

2) определить диаметр круглого сечения балки или стороны прямоугольного сечения при h / b = 2.

 

 

 

 

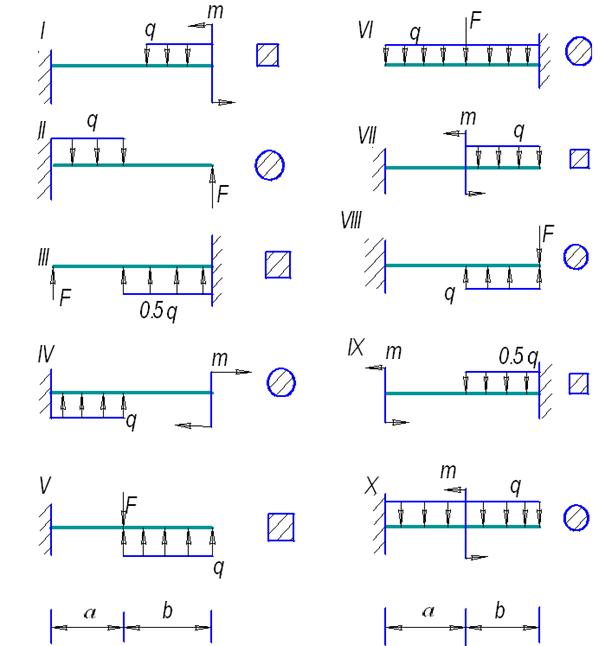
Рис. 28. Схемы балок к задаче 6

 

 

Таблица 7

Данные к задаче 6

Номер строки	Номер схемы	Нагрузки	Длины участков, м
F, кН	М, кН∙м	q, кН/м	а	в
	I			5,1	1,1	1,1
	II			5,2	1,2	1,2
	III			5,3	1,3	1,3
	IV			5,4	1,4	1,4
	V			5,5	1,5	1,5
	VI			5,6	0,6	0,6
	VII			5,7	0,7	0,7
	VIII			5,8	0,8	0,8
	IX			5,9	0,9	0,9
	X			6,0	1,0	1,0
	в	а	б	в	б	в

 

 

Задача 7. Плоский изгиб (двухопорная балка)

Произвести расчет на прочность двухопорной балки (рис. 29).

Материал балки – сталь, [σ_и] = 200 МПа.

План решения задачи:

1) определить опорные реакции и проверить правильность их определения;

2) построить эпюры поперечных сил и изгибающих моментов;

3) подобрать номер профиля сечения.

Исходные данные к задаче 7 приведены в табл. 8.

 

 

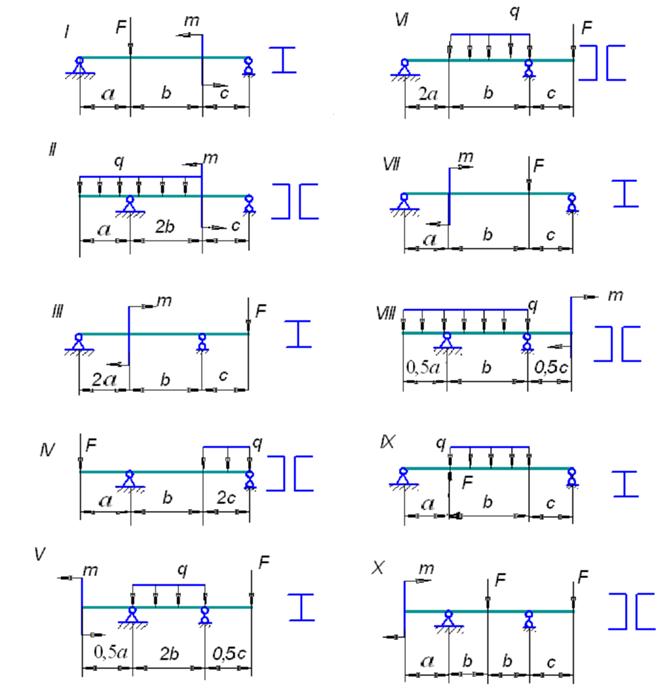
Рис. 29. Схемы балок к задаче 7

 

 

Таблица 8

Данные к задаче 7

 

Номер строки	Номер схемы	Нагрузки	Длины участков, м
F, кН	М, кНм	q, кН/м	а	в	с
	I				1,1	1,1	1,1
	II				1,2	1,2	1,2
	III				1,3	1,3	1,3
	IV				1,4	1,4	1,4
	V				1,5	1,5	1,5
	VI				1,6	1,6	1,6
	VII				1,7	1,7	1,7
	VIII				1,8	1,8	1,8
	IX				1,9	1,9	1.9
	X				2,0	2,0	2,0
	в	а	б	в	а	б	в

 

 

---

Дата добавления: 2014-11-13; просмотров: 27; Нарушение авторских прав

---

⇐ Предыдущая11121314151617181920Следующая ⇒