Глава 5. МОМЕНТЫ ИНЕРЦИИ ПЛОСКИХ СЕЧЕНИЙ

Любое плоское сечение характеризуется рядом геометрических характеристик: площадью, координатами центра тяжести, статическим моментом, моментом инерции и др.

Статические моменты относительно осей х и y равны:

, .

Статические моменты обычно выражаются в кубических сантиметрах или метрах и могут иметь как положительные, так и отрицательные значения. Ось, относительно которой статический момент равен нулю, называется центральной. Точка пересечения центральных осей называется центром тяжести сечения. Формулы для определения координат центра тяжести x_c и y_c сложного сечения, разбитого на простейшие составные части, для которых известны площади А_i и положение центра тяжести x_ci и y_ci, имеют вид

, .

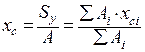Величина момента инерции характеризует сопротивляемость стержня деформации (кручения, изгиба) в зависимости от размеров и формы поперечного сечения. Различают моменты инерции:

– осевые, определяемые интегралами вида

, ;

– полярный:

;

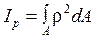– центробежный:

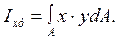
Осевые и полярные моменты инерции всегда положительны и не

обращаются в нуль. Полярный момент инерции I_p равен сумме осевых моментов инерции I_х и I_у относительно любой пары взаимно перпендикулярных осей х и у:

I_х + I_у = I_p = const.

Центробежный момент инерции может быть положительным, отрицательным и равным нулю. Размерность моментов инерции — см⁴ или м⁴. Формулы для определения моментов инерции простых сечений относительно центральных осей приведены в справочниках. При вычислении моментов инерции сложных сечений часто используют формулы перехода от центральных осей простых сечений к другим осям, параллельным центральным.

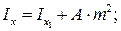
где 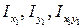– моменты инерции простых сечений относительно центральных осей;

m, n – расстояния между осями (рис. 18).

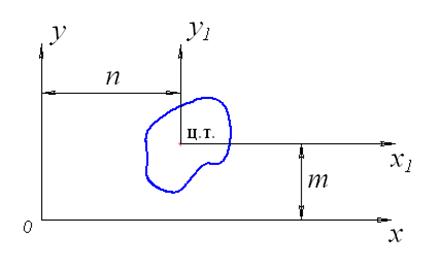
Рис. 18. К определению моментов инерции относительно осей,

параллельных центральным

Важное значение имеют главные центральные оси сечения. Главными центральными называются две взаимно перпендикулярные оси, проходящие через центр тяжести сечения, относительно которых центробежный момент инерции равен нулю, а осевые моменты инерции имеют экстремальные значения. Главные моменты инерции обозначаются I_u(max) и I_v(min) и определяются по формуле

.

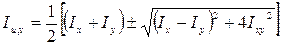Положение главных осей определяется углом α₀ , который находится из формулы

.

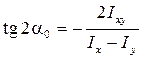Угол α₀ откладывается от оси с большим неглавным моментом инерции; положительное значение – против часовой стрелки.

Если сечение имеет ось симметрии, то эта ось является главной. Другая главная ось перпендикулярна оси симметрии. На практике часто используются сечения, составленные из нескольких прокатных профилей (двутавр, швеллер, уголок). Геометрические характеристики этих профилей приведены в таблицах сортамента. Для неравнобокого и равнобокого уголков центробежный момент инерции относительно центральных осей, параллельных полкам, определяется по формуле

.

Обратите внимание на обозначение главных центральных осей в таблице сортамента для уголков. Знак I_xy для уголка зависит от положения его в сечении. На рис.19 показаны возможные положения уголка в сечении и приведены знаки для I_xy.

Рис. 19. Возможные положения уголка в сечении

и знаки для I_xy

Пример 5

Определить I_u , I_v и положение главных центральных осей сечения

(рис. 20).

Сложное сечение состоит из двух прокатных профилей. Выписка из таблиц сортамента (прил. 5) приведена на рис. 21.

В качестве вспомогательных примем оси, проходящие по внешним

сторонам швеллера (оси x_B, y_B, см. рис. 20).Координаты центра тяжести сечения:

;

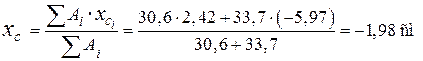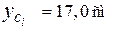(вычислите самостоятельно).

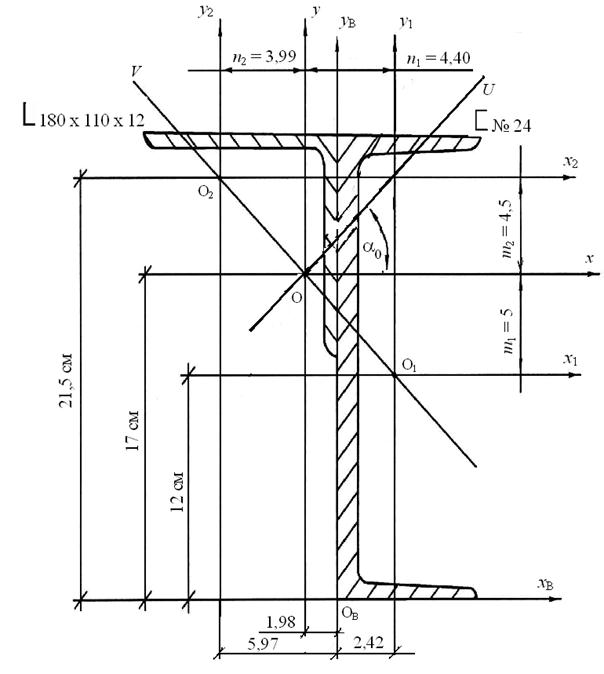
Рис. 20. Положение главных центральных осей инерции

U и V сложного сечения

В качестве вспомогательных можно было бы выбрать, например, центральные оси швеллера. Тогда несколько сократится объем вычислений.

Осевые моменты инерции:

.

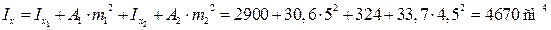Обратите внимание, что неравнобокий уголок в сечении расположен

иначе, чем показано в таблице сортаментов. Значение 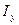вычислите самостоятельно .

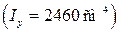№ 24 180 x 110 x 12

A = 30,6 см² A = 33,7 см²

I_x = 2900 см⁴ I_x = 1123 см⁴

I_y = 208 см⁴ I_y = 324 см⁴

z₀ = 2,42 см I_x(min)=194 см⁴

х₀=2,52см, y₀=5,97 см

Рис. 21. Значения геометрических характеристик прокатных профилей:

а – швеллера № 24; б – неравнобокого уголка 180 x 110 x 12

Центробежные моменты инерции:

– для швеллера (есть оси симметрии);

– для уголка ,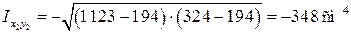

знак минус – в связи с положением уголка в сечении;

– для всего сечения:

.

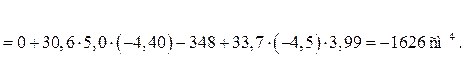
Проследите назначение знаков у n и m. От центральных осей швеллера переходим к общим центральным осям сечения, поэтому + m₂

и – n₂.

При переходе от осей x₂y₂ к осям xy будет: – m₂ и n₂.

Главные моменты инерции сечения:

;

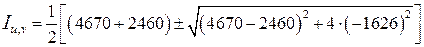
I_u = 5,53∙10³ cм⁴ = 5,53∙10^–5 м⁴;

I_v =1,6∙10³ cм⁴ = 1,6∙10^–5 м⁴ .

Положение главных центральных осей сечения:

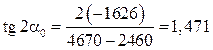; α₀ = 55^о48^′;

α₀ = 27^о54^′.

Угол α₀ отсчитывается от оси x, так как I_x > I_y.

Проверка правильности вычисления величин I_u, I_v и α₀ производится по формуле

.

Угол α₀ для этой формулы отсчитывается от оси u.

,

значит, операции по вычислению I_u, I_v, и α₀ произведены правильно.

Рассмотренное сечение имеет наибольшую сопротивляемость изгибу относительно оси u и наименьшую – относительно оси v.