
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Решение систем линейных уравнений
Система линейных уравнений n-го порядка имеет вид:
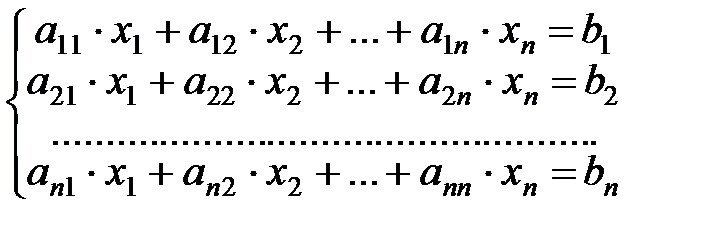
или в матричном виде:
A× X = B,
где  ,
,  ,
, 
Корнями системы являются такие значения x1, x2, … xn, подстановка которых превращает уравнения системы в тождества.
Матричный метод. Зная матрицу A можно вычислить обратную матрицу A-1, затем умножить ее на систему: A–1× A × X = A– 1× B.
Получится: X = A–1× B . Элементы вектора X и являются корнями системы линейных уравнений.
Чтобы решить систему в приложении Mathcad матричным методом, надо записать коэффициенты системы − матрицу A. Далее задается вектор B и записывается формула для определения корней
X := A–1× B
Корни вычисляются после набора выражения: X=
В приложении Excelтакже можно использовать матричный метод. Пусть имеется система линейных уравнений третьего порядка. Первоначально необходимо ввести элементы матрицы А, например, в ячейки А1:С3. Затем − вектор В, например, в ячейки Е1:Е3. Далее следует выделить диапазон ячеек для вычисления корней, например G1:G3 и в строке состояния набрать формулу:
=МУМНОЖ(МОБР(A1:C3);E1:E3)
После ее набора нажать не одну клавишу ввода, а вместе три клавиши: <Shift> + <Ctrl> + <Enter>. В ячейках G1:G3 появятся корни системы линейных уравнений.
Содержание заданий
1. Вычислить определенный интеграл для данных, приведенных в табл. 10.1 в приложении Mathcad.
2. Отделить корни уравнения f(x) = 0, где f(x) берется из той же табл. 10.1.
3. Найти корни уравнения в приложении Excel с помощью команды Подбор параметраив приложении Mathcad. Результаты сравнить между собой.
6. Решить произвольную систему линейных уравнений в приложениях Mathcad и Excel.
Таблица 10.1
| № вар. | Функция f(x) | Пределы интегрирования | № вар. | Функция f(x) | Пределы интегрирования |
| x2 + 4x – 2 | a = 1, b = 2 | x3 + 3x – 1 | a = 4, b = 8 | ||
| ln(x) + x – 3 | a = 3, b = 4 | x3 + x - 4 | a = 3, b = 4 | ||
| x3 + 2x – 1 | a = 6, b=7 | ln(x) + x3 | a = 3, b = 7 | ||
| 2ln(x) – 1/x | a = 8, b = 9 | ex – 2x2 -– 1 | a = 2, b = 9 | ||
| 2 – x 2 + x | a = 1, b = 3 | 2x + ln(x) – 7 | a = 2, b = 4 | ||
| 5x – 1 + x3 | a = 2, b = 5 | x3 + 2x – 4 | a = 1, b = 5 | ||
| 1 + ex + x | a = 3, b = 8 | 2 + x + ln(x) | a = 3, b = 7 | ||
| x3 + x – 2 | a = 6, b = 9 | x3 + x – 3 | a = 6, b = 8 |
Дата добавления: 2014-11-13; просмотров: 259; Мы поможем в написании вашей работы!; Нарушение авторских прав |