Формула полной вероятности. Пусть некоторое событие А может произойти вместе с одним из несовместных событий , составляющих полную группу событий

Пусть некоторое событие А может произойти вместе с одним из несовместных событий , составляющих полную группу событий. Пусть известны вероятности этих событий и условные вероятности наступления события А при наступлении события H_i .

Теорема. Вероятность события А, которое может произойти вместе с одним из событий , равна сумме парных произведений вероятностей каждого из этих событий на соответствующие им условные вероятности наступления события А.

Фактически эта формула полной вероятностиуже использовалась при решении примеров, приведенных выше, например, в задаче с револьвером.

Доказательство.

Т.к. события образуют полную группу событий, то событие А можно представить в виде следующей суммы:

Т.к. события несовместны, то и события AH_i тоже несовместны. Тогда можно применить теорему о сложении вероятностей несовместных событий:

При этом

Окончательно получаем:

Теорема доказана.

Пример. Один из трех стрелков производит два выстрела. Вероятность попадания в цель при одном выстреле для первого стрелка равна 0,4, для второго – 0,6, для третьего – 0,8. Найти вероятность того, что в цель попадут два раза.

Вероятность того, что выстрелы производит первый, второй или третий стрелок равна .

Вероятности того, что один из стрелков, производящих выстрелы, два раза попадает в цель, равны:

- для первого стрелка: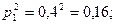

- для второго стрелка:

- для третьего стрелка:

Искомая вероятность равна: