
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Вариационные ряды. Генеральная совокупность и выборка
Совокупность предметов или явлений, объединённых каким – либо общим признаком или свойством качественного или количественного характера, называется объектом наблюдения.
- Количественным называется признак, значения которого выражаются числами.
- Качественным называется признак, характеризующийся некоторым свойством или состоянием элементов совокупности.
Каждый объект статистического наблюдения состоит из отдельных элементов – единиц наблюдения. Результаты статистических наблюдений представляют собой числовую информацию – данные.
Статистические данные – это сведения о том, какие значения принял интересующий исследователя признак в статистической совокупности.
Статистическая совокупность называется генеральной совокупностью, если исследованию подлежат все элементы совокупности.
Выборочной совокупностью, или просто выборкой, называют часть элементов генеральной совокупности подлежащих исследованию. Она извлекается из генеральной совокупности случайно, чтобы каждый объект имел равные шансы быть отобранным.
Значения признака, которые при переходе от одного элемента совокупности к другому изменяются, называются вариантами и обозначаются маленькими латинскими буквами. Порядковый номер варианта называется рангом.
Ряд значений признака, расположенный в порядке возрастания или убывания с соответствующими им весами, называется вариационным рядом.
В качестве весов выступают частоты или частости.
Частота (mi) показывает, сколько раз встречается тот или иной вариант в статистической совокупности.
Частость или относительная частота (wi) показывает, какая часть единиц совокупности имеет тот или иной вариант к сумме всех частот ряда. Частость рассчитывается как отношение частоты того или иного варианта к сумме всех частот ряда
(1) 
Сумма всех частостей равна 1
(2) 
Вариационные ряды бывают дискретными и интервальными.
Дискретные вариационные ряды строят обычно в том случае, если значения изучаемого признака могут отличаться друг от друга не менее чем на некоторую конечную величину. В дискретных вариационных рядах задаются точечные значения признака. Общий вид дискретного ряда показан в таблице.
| Значения признака (хi) | х1 | х2 | … | хk |
| Частоты (mi) | m1 | m2 | … | mk |
Интервальные вариационные ряды строят обычно в том случае, если значения изучаемого признака могут отличаться друг от друга на сколь угодно малую величину. Значения признаков в них задаются в виде интервалов. Общий вид интервального ряда имеет вид
| Значения признака (хi) | a1 – a2 | a2 – a3 | … | ai-1 - ai |
| Частоты (mi) | m1 | m2 | … | mi |
В интервальных вариационных рядах в каждом интервале выделяют верхнюю и нижнюю границы.
Разность между верхней и нижней границами интервала называется интервальной разностью или длиной интервала. В общем виде интервальную разность ki представим как
ki = xi (max) - xi (min)
Первый и последний интервалы могут быть открытыми, т.е. иметь только одну границу.
Если интервалы в вариационных рядах имеют одинаковую длину, их называют равновеликими, в противном случае неравновеликими.
При построении интервального ряда (если строится ряд с равными интервалами), для определения оптимальной величины интервалов применяют формулу Стэрджесса
 ,
,
где n число единиц совокупности; x max и x min – наибольшее и наименьшее значения вариационного ряда.
Дискретный вариационный ряд графически можно представить с помощью полигона распределения частот или частостей. рис.8

рис.8
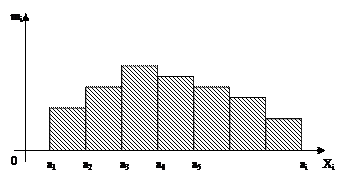 Интервальные вариационные ряды графически можно представить в виде гистограмм, т. е. столбчатой диаграммы. рис.9
Интервальные вариационные ряды графически можно представить в виде гистограмм, т. е. столбчатой диаграммы. рис.9
рис.9
Абсолютная плотность – это отношение частоты интервала к его величине:
 ,
,
где  - абсолютная плотность i – го интервала; mi – его частота; ki – интервальная разность. Абсолютная плотность показывает, сколько единиц совокупности приходится на единицу интервала.
- абсолютная плотность i – го интервала; mi – его частота; ki – интервальная разность. Абсолютная плотность показывает, сколько единиц совокупности приходится на единицу интервала.
Относительная плотность – отношение частости интервала к его величине:
 ,
,
где  -относительная плотность i – го интервала;
-относительная плотность i – го интервала;
Относительная плотность показывает, какая часть единиц совокупности приходится на единицу интервала.
 2. Числовые характеристики вариационного ряда
2. Числовые характеристики вариационного ряда
Одной из основных характеристик ряда распределения является средняя арифметическая. Существует две формулы для расчёта средней арифметической: простая и взвешенная. Простую среднюю арифметическую используют, когда данные наблюдений не сведены в вариационный ряд или все частоты равны единице (одинаковы).
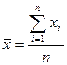 ,
,
где хi – i-е значение признака; n – объём ряда (число наблюдений).
Если частоты отличны друг от друга, расчёт производится по формуле средней арифметической взвешенной

где хi – i-е значение признака; mi – частота i-го значения признака; k – число его значений (вариантов).
При расчёте средней арифметической в качестве весов могут выступать и частости, тогда формула расчёта средней арифметической взвешенной примет следующий вид.

где wi – частость i-го значения признака;
Колеблемость изучаемого признака можно охарактеризовать с помощью различных показателей вариации. К числу основных показателей вариации относятся: математическое ожидание, дисперсия, среднее квадратическое отклонение, коэффициент вариации.
Математическое ожидание – это числовая характеристика случайной величины, со средним арифметическим её наблюдаемых значений, которое является статистической характеристикой вариационного ряда и рассчитывается по формуле:

где рi – вероятность i-го значения признака.
Дисперсию можно рассчитать по простой и взвешенной формулам имеющим вид
 ;
; 

Среднее квадратическое отклонение рассчитывается по формуле

Коэффициент вариации определяется формулой
 .
.
Тестовые вопросы для самоконтроля:
1. Объем выборки, это :
а) сумма всех вариант б) сумма всех частот
в) относительная частота
2.Наглядное представление для непрерывных распределений дает
а) полигон б) пучок прямых в) гистограмма
Значения эмпирической функции:
а) принадлежат отрезку [0;1]
б) принадлежат интервалу (0;+∞) в) равны 0,5
Среднее арифметическое наблюдаемых значений выборки сходится по вероятности к:
а) математическому ожиданию случайной величины
б) объему выборки в) медиане
Для описания рассеивания наблюдаемых значений случайной величины используется:
а) среднее арифметическое
б) среднее квадратическое отклонение и дисперсия
в) мода и медиана
Вычислите среднее арифметическое на основе выборки:
| Хi | |||||
| ni |
а) 15 б) 1/65 в) 58/13
Для предыдущей выборки найдите медиану:
а) 4 б) 3 и 5 в) 5
Рекомендуемая литература
Основная:
1. Тырсин, А. Н. Математика.Теория вероятностей и математическая статистика [Текст] : учебное пособие/ А. Н. Тырсин.- Челябинск : Челяб. гос. ун-т, 2007.- 235 c.
2. Общий курс высшей математики для экономистов [Текст]: Учебник /Под ред. В. И. Ермакова.- М.: Инфра-М, 2008.- 656 с.- Гриф МО
Дополнительная:
1. Сборник задач по высшей математике для экономистов [Текст]: Учебное пособие.- 2-е изд., испр.- М.: Инфра-М, 2008.- 574 с.- Гриф УМО
Дата добавления: 2014-12-03; просмотров: 840; Мы поможем в написании вашей работы!; Нарушение авторских прав |