Нахождение выборочного уравнения прямой линии регрессии.

Данные о статистической зависимости удобно задавать в виде корреляционной таблицы.

Рассмотрим задачу: Экономист, анализируя зависимость между рыночными ценами У и размерами предложения Х некоторого товара, обследовал 100 торговых точек и получил следующие данные:

Х У							nУ
3,6
4,9
6,2
7,5
8,8
nX

Полагая, что между Х и У имеет место линейная связь,

найти линейное уравнение регрессии

Решение: Составим корреляционную таблицу в условных вариантах u_i ; v_j : u_{i =} , где h₁=10, h₂=13,

C₁, C₂- ложные нули. В качестве ложных нулей выбираем варианты либо расположенные примерно в середине соответствующего вариационного ряда, либо имеющие наибольшую частоту. В нашей задаче С₁=51, С₂=6,2

u	-3	-2	-1
-2
-1

Вычислим и

Найдем вспомогательные величины

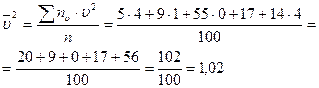
Вычислим и :

Найдем , для этого составим расчетную таблицу:

u	-3	-2	-1				U
-2	-9 -6	-4 -4					-13
-1		-12 -6	-3 -3				-15
			-4
			-2
V	-6	-10	-1
								контроль

Искомая сумма

Найдем выборочный коэффициент корреляции

связь тесная, т.к. 0,65 < r < 0,8

Вычислим 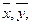учитывая, что С₁ = 51, С₂ = 6.2

h₁=10, h₂=1,3

Определим σ_х=σ_u·h₁ = 0,98·10=9,8

σ_y = σ ·h₂ = 0,96·1,3 = 1,248 ≈ 1,25

Найденные значения подставляем в уравнение прямой линии регрессии

Коэффициент корреляции значимо отличается от нуля, следовательно Х и У коррелированны.

4. Коэффициент корреляции и его свойства

Чтобы на практике обнаружить наличие линейной зависимости между двумя величинами и оценить степень точности этой зависимости, необходимо знание коэффициента линейной корреляции. Он находится по формуле

или 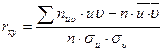(в условных вариантах )

Свойства коэффициента корреляции.

1. Коэффициент линейной корреляции изменяется в пределах от –1 до 1

/r_xy/ ≤ 1

2. Если зависимость между Х и У отсутствует, то r_xy=0. Обратное утверждение, вообще говоря, несправедливо: равенство нулю r_xy не означает отсутствия зависимости между Х и У, оно лишь сигнализирует об отсутствии линейной зависимости.

3. На практике приняты следующие пределы качественной характеристики тесноты связи:

/r_xy/ ≤ 0- связь между Х и У отсутствует или не является линейной даже приближенного,

0,1 < /r_xy/ ≤ 0,3 – связь слабая,

0,3 < /r_xy/ ≤0,65 – связь средней тесноты,

0,65</r_xy/ ≤0,8 - связь тесная

0,8</r_xy/ ≤0,95 –связь очень тесная

/r_xy/>0,96 – связь между Х и У считается функциональной.

Значит, чем больше /r_xy/, тем точнее результаты, получаемые с помощью уравнения прямой регрессии.

Данные, с помощью которых вычитывается r_xy и строится уравнение связи между Х и У, носят случайный характер.

Проверить связь на случайность можно с помощью корреляционной поправки

,

где r = r_xy, n- объем выборки.

Установлено, что если связь между Х и У существенная, то / ≥ 3

Вопросы для самоконтроля

1. Что называют корреляционной зависимостью?

2. Как называется условное математическое ожидание случайной

величины У при Х=х, т. М_х (У)?

3. Существует ли связь между Х и Y, если коэффициент корреляции /r_xy/ ≤0?

4. Чему равен коэффициент корреляции, если связь между Х и У считается средней тесноты?

Рекомендуемая литература

Основная:

1. Тырсин, А. Н. Математика.Теория вероятностей и математическая статистика [Текст]: учебное пособие/ А. Н. Тырсин.- Челябинск: Челяб. гос. ун-т, 2007.- 235 c.

2. Кремер, Н.Ш. Теория вероятностей и математическая статистика [Текст]: Учебник.-2-е изд., перераб. и доп.- М.: ЮНИТИ, 2006.-573 с.- Гриф МО

Дополнительная:

1. Общий курс высшей математики для экономистов [Текст]: Учебник /Под ред. В. И. Ермакова.- М.: Инфра-М, 2008.- 656 с.- Гриф МО

2. Сборник задач по высшей математике для экономистов [Текст]: Учебное пособие.- 2-е изд., испр.- М.: Инфра-М, 2008.- 574 с.- Гриф УМО