Коэффициенты уравнения парной линейной регрессии

Как уже было определено выше, в случае линейной зависимости уравнение регрессии является уравнением прямой линии. Таких уравнений два:

Y = a₁ + b_y/xX — прямое

и X = a₂ + b_x/yY — обратное, (2)

где: a и b – коэффициенты, или параметры, которые надлежит определить.
Значение коэффициентов регрессии вычисляется по формуле:

и . (3)

Коэффициенты регрессии b имеют размерность, равную отношению размерностей изучаемых показателей X и Y, и тот же знак, что и коэффициент корреляции.

Коэффициенты а определяются по формуле:

и . (4)

Чтобы вычислить эти коэффициенты, надо просто в уравнения регрессии подставить средние значения коррелируемых переменных.
Для оценки качества уравнений регрессии вычисляются остаточные средние квадратические отклонения (или абсолютные погрешности уравнений) по формуле:

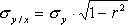
и . (5)

Эти оценки абсолютны и, следовательно, не могут быть сравнимы друг с другом. Поэтому вводят оценки относительной погрешности уравнений, которые выражаются в процентах и служат для точности предсказания (прогнозирования) результатов одного показателя по заранее известным значениям другого. Относительные погрешности уравнений регрессии определяются по формуле:

и . (6)

Значение этой оценки, если r = , равно нулю и, если r = 0, максимально. Остаточное среднее квадратическое отклонение характеризует колеблемость Y относительно линии регрессии по Х в прямом уравнении регрессии и, наоборот, в обратном случае. А, следовательно, чем меньше величина относительной погрешности уравнения регрессии, тем точнее будет оно осуществлять прогноз значений одного показателя по заранее известным значениям другого.

4. Связь между коэффициентами регрессии и корреляции
Между коэффициентом корреляции и параметром парной линейной регрессии существует зависимость, которая применительно к выборочным оценкам может быть представлена следующим образом:

, (7)

где: и _y, _x- средние квадратические ошибки.
Приведенное выражение позволяет оценить параметр регрессии без решения системы нормальных уравнений при условии, что коэффициент корреляции уже определен. Выборочный коэффициент корреляции равен среднему геометрическому выборочных коэффициентов регрессии. Действительно, Сравнив формулы (9.3) с основной формулой (8.1) коэффициента корреляции, видим, что их числители равны . Это свидетельствует об определенной связи между этими характеристиками. Выборочный коэффициент корреляции выражается тогда равенством r2 = by/x * bx/y , откуда

. (8)

Эта формула ценна тем, что, во-первых, может быть использована для нахождения неизвестной величины коэффициента корреляции по известным значениям коэффициента регрессии by/x и bx/y, а во-вторых, позволяет контролировать правильность расчета коэффициента корреляции, если известны величины by/x и bx/y. Знак выборочного коэффициента корреляции совпадает со знаком выборочных коэффициентов регрессии. Если зависимость между признаками функциональная, то by/x = 1 / bx/y и, следовательно, r = 1. И, наоборот, при полном отсутствии взаимосвязи между признаками by/x= 0, bx/y= 0, и r = 0.