Понятие регрессии

В практических исследованиях возникает необходимость аппроксимировать (описать приблизительно) диаграмму рассеяния математическим уравнением. То есть зависимость между переменными величинами Y и Х можно выразить аналитически с помощью формул и уравнений и графически в виде геометрического места точек в системе прямоугольных координат. График корреляционной зависимости строится по уравнениям функци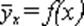и и , которые называются регрессией (термин “регрессия” происходит от лат. Regressio - движение назад). Здесь и 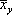- средние арифметические из числовых значений зависимых переменных Y и X.
Для выражения регрессии служат эмпирические и теоретические ряды, их графики - линии регрессии, а также корреляционные уравнения (уравнения регрессии) и коэффициент линейной регрессии.
Показатели регрессии выражают корреляционную связь двусторонне, учитывая изменение средней величины признака Y при изменении значений xi признака X, и, наоборот, показывают изменение средней величины признака Х по измененным значениям yi признака Y. Исключение составляют временные ряды, или ряды динамики, показывающие изменение признаков во времени. Регрессия таких рядов является односторонней.

Основная задача регрессионного анализа- установление формы связи между переменными.

Ряды регрессии, особенно их графики, дают наглядное представление о форме и тесноте корреляционной связи между признаками, в чем и заключается их ценность. Форма связи между показателями может быть разнообразной. И поэтому задача состоит в том, чтобы любую форму корреляционной связи выразить уравнением определенной функции (линейной, параболической и т.д.), что позволяет получать нужную информацию о корреляции между переменными величинами Y и X, предвидеть возможные изменения признака Y на основе известных изменений X, связанного с Y корреляционно.

2. Уравнение линейной регрессии
Обычно признак Y рассматривается как функция многих аргументов - x₁, x₂, x₃, -и может быть записана в виде:

y = a + bx₁ + cx₂ + dx₃ + ... ,

где: а, b, с и d - параметры уравнения, определяющие соотношение между аргументами и функцией. В практике учитываются не все, а лишь некоторые аргументы, в простейшем случае, как при описании линейной регрессии, - всего один:

y = a + bx (1)

В этом уравнении параметр а - свободный член; графически он представляет отрезок ординаты (у) в системе прямоугольных координат. Параметр b называется коэффициентом регрессии. С точки зрения аналитической геометрии b - угловой коэффициент, определяющий наклон линии регрессии по отношению к осям, координат. В области регрессионного анализа этот параметр показывает, насколько в среднем величина одного признака (Y) изменяется при изменении на единицу меры другого корреляционно связанного с Y признака X. Наглядное представление об этом параметре и о положении линий регрессии Y по Х и X по Y в системе прямоугольных координат дает рисунок 1.

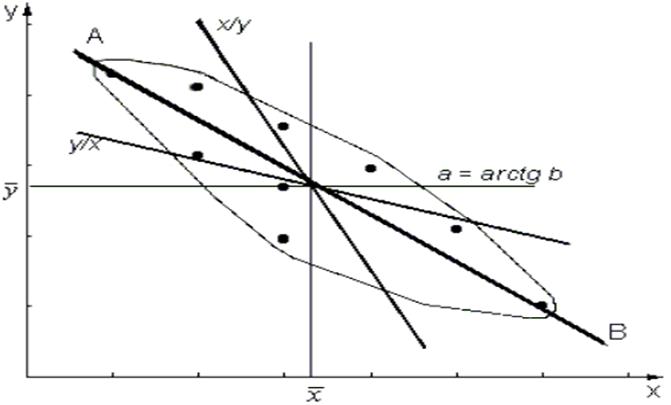
Рис. 1. Схема линий регрессии Y по Х и Х по Y в системе прямоугольных координат.

Линии регрессии, как показано, пересекаются в точке 0 ( ), соответствующей средним арифметическим значениям корреляционно связанных друг с другом признаков Y и X. Линия АВ, проходящая через эту точку, изображает полную (функциональную) зависимость между переменными величинами Y и X, когда коэффициент корреляции r = 1. Чем сильнее связь между Y и X, тем ближе линии регрессии к АВ, и, наоборот, чем слабее связь между варьирующими признаками, тем более удаленными оказываются линии регрессии от АВ. При отсутствии связи между признаками, когда r = 0, линии регрессии оказываются под прямым углом (90°) по отношению друг к другу.
Уравнение регрессии тем лучше описывает зависимость, чем меньше рассеяние диаграммы, чем больше теснота взаимосвязи. Уравнение прямой линии пригодно для описания только линейных зависимостей. В случае не-линейных зависимостей математическая запись может отображаться уравнениями параболы, гиперболы и др.

Необходимо также сделать одно важное замечание о значении показателей, характеризующих взаимосвязь признаков (коэффициентов корреляции, регрессии и т. п.).

Все они дают лишь количественную меру связи, но ничего не говорят о причинах зависимости. Определить эти причины - дело самого исследователя.