Графическое представление уравнения парной линейной регрессии

Эмпирические ряды регрессии Y по Х и Х по Y изображаются в виде линейного графика, при построении которого наиболее точным является использование способа наименьших квадратов, предложенного в 1806 г. К. Гауссом и независимо от него А. Лежандром. В основу этого способа положена теорема, согласно которой сумма квадратов отклонений вариант (x_i) от средней арифметической ( ) есть величина наименьшая, т. е. 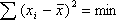Отсюда и название метода, который нашел широкое применение не только в биологии, но и в технике. Мы уже говорили об этом методе и применяли его, когда находили параметры а и b линейной регрессии, отыскивая эмпирическое уравнение.
При графическом изображении эмпирического уравнения регрессии (например, показатели роста и веса 10 исследуемых), представленного на рисунке 2 используется следующая последовательность:

1. Определив форму и направление взаимосвязи между эмпирическими данными на основе данных расчета нормированного коэффициента корреляции, производят расчет уравнений регресиии (прямого и обратного) по формуле (13).
2. Подставляя в конечный вид уравнений, выражающих зависимость между переменными величинами Y и X, эмпирические данные x_i и y_i находят координаты точек линий регрессии для усредненных значений y_x и x_y.
3. На графике, выполненном в прямоугольной системе координат, на оси x откладывают значения переменных x_i, на оси у – значения y_i и отмечают точками рассчитанные координаты линий регрессии для усредненных значений y_x и x_y (рис. 2).
4. Две линии регрессии на графике пересекаются в точке М с координатами средних значений показателей x_i и y_i.

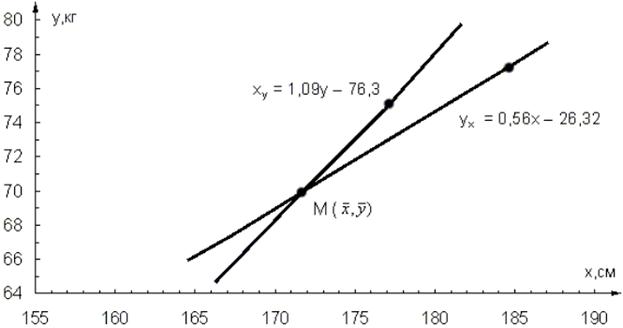
Рис.2. Графическое изображение эмпирического уравнения регрессии.
График линий регрессии отражает ряды теоретически ожидаемых значений функции по известным значениям аргумента. При этом, чем сильнее взаимосвязь между величинами x_i и y_i, тем меньше угол между линиями регрессии. При r = линии уравнения регресии либо совпадают, либо расположены параллельно, так как корреляционная зависимость между признаками в этом случае переходит в функциональную. И, наоборот, чем слабее зависимость между признаками, тем больше угол между линиями на графике. При r = 0 линии регрессии расположены перпендикулярно.

Вопросы для самоконтроля:

1. Дайте определение регрессии.

2. Что выражают показатели регрессии?

3. Какой вид имеет уравнение регрессии?

4. Приведите основные формулы регрессионного анализа

5. Какая связь существует между коэффициентами корреляции и регрессии?

Рекомендуемая литература

Основная:

1. Тырсин, А. Н. Математика.Теория вероятностей и математическая статистика [Текст]: учебное пособие/ А. Н. Тырсин.- Челябинск : Челяб. гос. ун-т, 2007.- 235 c.

Дополнительная:

1. Общий курс высшей математики для экономистов [Текст]: Учебник /Под ред. В. И. Ермакова.- М.: Инфра-М, 2008.- 656 с.- Гриф МО

2. Сборник задач по высшей математике для экономистов [Текст]: Учебное пособие.- 2-е изд., испр.- М.: Инфра-М, 2008.- 574 с.- Гриф УМО