
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Автокорреляционная функция
Так как коэффициент ρ(τ) измеряет корреляцию между членами одного и того же ряда, его называют коэффициентом автокорреляции, а зависимость ρ(τ) – автокорреляционной функцией. В силу стационарности временного ряда хt (t=1,2,…,n) автокорреляционная функция ρ(τ) зависит только от лага τ, причем ρ(-τ) = ρ(τ), т.е. при изучении ρ(τ) можно ограничиться рассмотрением только положительных значений τ.
Статистической оценкой ρ(τ) является выборочный коэффициент автокорреляции rτ, определяемый по формуле коэффициента корреляции, в которой хi = хt, уi = хt+τ, а п заменяется на п-τ:
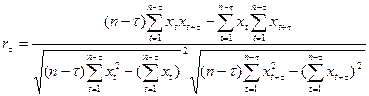 (4)
(4)
Функцию rτ называют выборочной автокорреляционной функцией, а её график – коррелограммой.
При расчете rτ следует помнить, что с увеличением τ число п-τ пар наблюдений хt , хt+τ уменьшается, поэтому лаг τ должен быть таким, чтобы число п-τ было достаточным для определения rτ . Обычно ориентируются на соотношение τ≤п/4.
Для стационарного временного ряда с увеличением лага τ взаимосвязь членов временного ряда хt и хt+τ ослабевает и автокорреляционная функция ρ(τ) должна убывать (по абсолютной величине). В то же время для её выборочного (эмпирического) аналога rτ , особенно при небольшом числе пар наблюдений п-τ, свойство монотонного убывания (по абсолютной величине) при возрастании τ может нарушаться.
Пример 1.По данным таблицы 1 для временного ряда уt найти среднее значение, среднее квадратическое отклонение и коэффициенты автокорреляции (для лагов τ =1;2).
Р е ш е н и е. Среднее значение временного ряда находим по формуле (1)
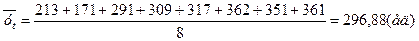
Дисперсию и среднее квадратическое отклонение можно вычислить по формуле (2), но в данном случае проще использовать соотношение
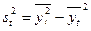 = 92 478,38-296,882= 4343,61;
= 92 478,38-296,882= 4343,61;
st =  = 65.31 (ед)
= 65.31 (ед)
где 
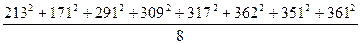 =
=
= 92 478,38
Найдем коэффициент автокорреляции rτ временного ряда (для лага τ =1), т.е. коэффициент корреляции между последовательностями семи пар наблюдений уt и уt+1 (t=1,2,…,7):
| уt | |||||||
| уt+τ |
Вычисляем необходимые суммы:
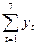 = 213+171+291+309+317+362+351=2014
= 213+171+291+309+317+362+351=2014
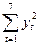 =2132+1712+2912+3092+3172+3622+3512=609 506
=2132+1712+2912+3092+3172+3622+3512=609 506
 =171+291+309+317+362+351+361=2162
=171+291+309+317+362+351+361=2162
 =1712+2912+3092+3172+3622+3512+3612= 694 458
=1712+2912+3092+3172+3622+3512+3612= 694 458
 = 213*171+171*291+291*309+309*317+317*362+362*351+351*361= = 642 583
= 213*171+171*291+291*309+309*317+317*362+362*351+351*361= = 642 583
Теперь по формуле (4) вычисляем коэффициент автокорреляции
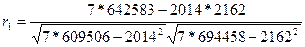 =0,725
=0,725
Вычисление коэффициента автокорреляции r2 временного ряда у(t) для лага τ =2, т.е. коэффициента корреляции между последовательностями шести пар наблюдений уt и уt+2(t=1,2,…,6) провести самостоятельно.
| уt | ||||||
| уt+τ |
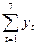 = 213+171+291+309+317+362 =1663
= 213+171+291+309+317+362 =1663
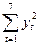 =2132+1712+2912+3092+3172+3622=486 305
=2132+1712+2912+3092+3172+3622=486 305
 = 291+309+317+362+351+361=1991
= 291+309+317+362+351+361=1991
 = 2912+3092+3172+3622+3512+3612= 665217
= 2912+3092+3172+3622+3512+3612= 665217
 = 213*291+171*309+291*317+309*362+317*351+362*361 = 560876
= 213*291+171*309+291*317+309*362+317*351+362*361 = 560876
Теперь по формуле (4) вычисляем коэффициент автокорреляции
 =0,842
=0,842
Знание автокорреляционной функции rτ может оказать существенную помощь при подборе модели анализируемого временного ряда и статистической оценке её параметров.
Вопросы для самоконтроля:
- Что называют временным рядом?
- Что представляет собой сезонная компонента?
- Что представляет собой тренд
- Что представляет собой циклическая компонента
- Что представляет собой случайная компонента
- Что является классической задачей при исследовании экономических временных рядов?
- Какие ряды называют стационарными? Назовите их характеристики.
- Какой вид имеет автокорреляционная функция?
9. Что называют выборочной автокорреляционной функцией? Как называется её график?
Рекомендуемая литература
Основная:
1. Тырсин, А. Н. Математика.Теория вероятностей и математическая статистика [Текст]: учебное пособие/ А. Н. Тырсин.- Челябинск : Челяб. гос. ун-т, 2007.- 235 c.
Дополнительная:
1. Общий курс высшей математики для экономистов [Текст]: Учебник /Под ред. В. И. Ермакова.- М.: Инфра-М, 2008.- 656 с.- Гриф МО
2. Сборник задач по высшей математике для экономистов [Текст]: Учебное пособие.- 2-е изд., испр.- М.: Инфра-М, 2008.- 574 с.- Гриф УМО
Дата добавления: 2014-12-03; просмотров: 524; Мы поможем в написании вашей работы!; Нарушение авторских прав |