Синтез корректирующих звеньев.

5.1. Синтез корректирующих звеньев контура напряжения (тока).

Наибольшее распространение получил метод синтеза по ЛАЧХ, поэтому ниже даются основные положения по этому методу применительно к последовательным корректирующим звеньям. Исходные динамические показатели при синтезе контуров приведены в табл.1

Таблица 1. Динамические показатели САУ

Тип контура	Добротность	Время переходного процесса	Перерегулирование
РН(Т)	40-60
РС	30-50		%
РП		=0,05	=22

Приводится структурная схема контура. Главная обратная связь показывается единичной. Исходные данные берутся из табл. 7. Выполняется синтез корректирующего устройства. Приводятся необходимые графики ЛАЧХ и ФЧХ (синтезированного) контура.

Структурная схема исходного контура приведена на рис. 11.

Рис. 11. Структурная схема контура напряжения

Построение ЛАЧХ исходного контура. Передаточная функция исходного контура ранее определена и имеет вид

.

Вначале полагаем, что передаточная функция корректирующего звена равна единице

.

Требуемая добротность контура определена заданием (табл. 7.) и составляет 40. Строим ЛАЧХ исходного контура при добротности К=40 ( ).

Так как добротность исходного контура ниже требуемой, то коэффициент его передачи увеличивается за счет введения дополнительного усилителя с коэффициентом усиления

.

Сопрягающие частоты ЛАЧХ исходного контура:

; .

Построение желаемой ЛАЧХ. Контур должен иметь добротность К=45 с^-1 и показатели переходного процесса: ; .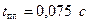

На оси частоты при откладывается точка .

Через точку проводится прямая под наклоном –20 дБ/дек.

Определяем частоту среза. Так как перерегулирование не задано, то

принимаем .

На частоте среза проводится прямая под наклоном -20 дБ/дек до значений = 11 дБ. При этом сопрягающие частоты будут

, .

Из точки ЛАЧХ на частоте проводится прямая под наклоном 0 дБ/дек до пересечения с низкочастотной частью ЛАЧХ. При этом определяется первая сопрягающая частота .

На частоте ω_Ж3 ЛАЧХ принимает наклон -40 дБ/дек и проводится до граничной частоты, которая определяется из условия , принимаем . Далее наклоны желаемой ЛАХ берутся равными наклонам исходной системы.

Соответствующая построенной желаемой ЛАЧХ передаточная функция контура будет .

где , , .

Определение передаточной функции корректирующего звена. ЛАЧХ корректирующего звена определяется как:

.

В результате по полученной ЛАЧХ записываем передаточную функцию корректирующего звена

.

Так как полученная передаточная функция не реализуется одним звеном, то разбиваем его на три

.

По результирующей ЛАЧХ корректирующего звена строится ЛАЧХ составляющих корректирующих звеньев .

; ; .

Выбор схемы корректирующих звеньев и определение значений входящих в нее элементов.

1. Рассмотрим для первого корректирующего звена с передаточной функцией

.

Звено интегродифференцирующее, постоянная времени числителя больше постоянной времени знаменателя. Выбираем схему электрическую принципиальную корректирующего звена (КЗ), описываемой такой передаточной функцией [2]. Схема КЗ приведена на рис. 12.

Выведем передаточную функцию этого звена. В результате вывода получаем .

Элементы схемы и параметры передаточной функции звена определяются следующими соотношениями

; ; .

Числовые значения коэффициента передачи и постоянных времени звена должны быть

, , .

Задаемся значением входного сопротивления цепочки 10 кОм, которое выбирается в диапазоне 5–10 кОм, что соответствует входным и выходным сопротивлениям нагрузки, применяемым в электроприводах усилителей и преобразователей.

Определяем числовое значение емкости конденсатора C1, мкФ

.

Определяем значение сопротивления : , откуда

.

В результате расчетов значения элементов корректирующей цепочки будут: , , .

Определяем коэффициент передачи корректирующего звена

.

Так как фактический коэффициент передачи полученного звена не совпадает с требуемым значением , то коэффициент передачи прямого тракта контура умножается на соответствующее значение , определяемое из условия , откуда .

2. Рассмотрим для второго корректирующего звена с передаточной функцией

.

Числовые значения коэффициента передачи и постоянных времени звена должны быть , , .

Определяем числовое значение емкости конденсатора C1, мкФ

.

Определяем значение сопротивления : ,откуда

.

В результате расчетов значения элементов корректирующей цепочки будут:

, , .

Определяем коэффициент передачи корректирующего звена, где 10 кОм,

Так как фактический коэффициент передачи полученного звена не совпадает с требуемым значением , то коэффициент передачи прямого тракта контура умножается на соответствующее значение , определяемое из условия , откуда .

3. Рассмотрим для третьего корректирующего звена с передаточной функцией .

Числовые значения коэффициента передачи и постоянных времени звена должны быть , , .

Определяем числовое значение емкости конденсатора C1, мкФ

.

Определяем значение сопротивления : , откуда

.

В результате расчетов значения элементов корректирующей цепочки будут:

, , .

Определяем коэффициент передачи корректирующего звена, где 10 кОм,

Так как фактический коэффициент передачи полученного звена не совпадает с требуемым значением , то коэффициент передачи прямого

тракта контура умножается на соответствующее значение , определяемое из условия , откуда .

5.2.Синтез корректирующих звеньев контура скорости.

Приводится структурная схема контура. Главная обратная связь показывается единичной. Исходные данные берутся из табл. 5. Выполняется синтез корректирующего устройства. Приводятся необходимые графики ЛАЧХ.

Структурная схема контура скорости приведена на рис.13.

Рис.13. Структурная схема контура скорости

Строим ЛАЧХ исходного контура L_u2(ω).Передаточная функция исходного контура имеет вид:

.

Определение ПФ замкнутого контура:

где .

Передаточная функция корректирующего звена равна единице

W_K3(p) = 1, тогда

.

Добротность для контура скорости принимаем К_ж = 30(20lg30=30дБ).

Т.к. добротность исходного контура ниже требуемой, то вводим усилитель с коэффициентом усиления:

.

Сопрягающие частоты ЛАЧХ исходного контура:

; ;

Строим желаемую ЛАЧХ L_ж2(ω).

Исходные данные:

- добротность контура К_ж =30[c^-1];

- время переходного процесса t_ппк2=0,0375 [c^-1];

- перерегулирование σ = 35%.

Низкочастотная область – на оси частот при ω = 1 откладываем точку 20lgК=20lg30=30[дБ] и через нее проводим горизонтальную прямую.

Среднечастотная область – частота среза:

.

Через точку ω_с = 440[c^-1] проводим прямую под наклоном -20 дБ/дек до значений L(ω) = ±11[дБ/дек]; ω_ж2 =90 [c^-1]; ω_ж3 = 900[c^-1].

Из точки ЛАЧХ на частоте проводится прямая под наклоном 0 дБ/дек до пересечения с низкочастотной частью ЛАЧХ. При этом определяется первая сопрягающая частота .

Высокочастотная область – на частоте ω_ж2 проводим прямую под наклоном -40 дБ/дек до граничной частоты ω_г = 5 ∙ ω_ж2 = 5 ∙900 = 4500 [c^-1], далее наклоны желаемой ЛАЧХ равны наклонам исходной системы.

ПФ желаемого контура:

.

Определение ПФ корректирующего звена.

ЛАЧХ корректирующего звена определяется как:

.

В результате по полученной ЛАЧХ L_к3(ω) записываем ПФ корректирующего звена:

Так как полученная передаточная функция не реализуется одним звеном, то разбиваем его на три

.

По результирующей ЛАЧХ корректирующего звена строится ЛАЧХ составляющих корректирующих звеньев :

; ; .

Выбор схемы корректирующих звеньев и определение значений входящих в нее элементов.

1. Рассмотрим для первого корректирующего звена с передаточной функцией

Числовые значения коэффициента передачи и постоянных времени звена должны быть , , . Определяем числовое значение емкости конденсатора C1, мкФ: .

Определяем значение сопротивления : .

В результате расчетов значения элементов корректирующей цепочки будут:

, , .

Определяем коэффициент передачи корректирующего звена, где 10 кОм,

Так как фактический коэффициент передачи полученного звена не совпадает с требуемым значением , то коэффициент передачи прямого тракта контура умножается на соответствующее значение , определяемое из условия , откуда .

2. Рассмотрим для второго корректирующего звена с передаточной функцией

.

Числовые значения коэффициента передачи и постоянных времени звена должны быть , , .Определяем числовое значение емкости конденсатора C1, мкФ: .

Определяем значение сопротивления : .

В результате расчетов значения элементов корректирующей цепочки будут:

, , .

Определяем коэффициент передачи корректирующего звена, где 10 кОм,

Так как фактический коэффициент передачи полученного звена не совпадает с требуемым значением , то коэффициент передачи прямого тракта контура умножается на соответствующее значение , определяемое из условия , откуда .

3. Рассмотрим для третьего корректирующего звена с передаточной функцией .

Числовые значения коэффициента передачи и постоянных времени звена должны быть , , 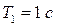. Определяем числовое значение емкости конденсатора C1, мкФ: .

Определяем значение сопротивления : .

В результате расчетов значения элементов корректирующей цепочки будут:

, , .

Определяем коэффициент передачи корректирующего звена, где 10 кОм,

Так как фактический коэффициент передачи полученного звена не совпадает с требуемым значением , то коэффициент передачи прямого тракта контура умножается на соответствующее значение , определяемое из условия , откуда .