Обратная матрица.

4.1. Какую матрицу называют обратной?

4.2. Для какой матрицы существует обратная?

4.3. Какой вид имеет обратная матрица?

4.4. Сформулируйте теорему об обратной матрице.

4.5. Перечислите этапы нахождения элементов обратной матрицы.

Метод Крамера.

5.1. Сформулируйте теорему Крамера и запишите формулы Крамера.

5.2. Перечислите этапы решения системы неоднородных линейных уравнений методом Крамера.

5.3. Для каких систем уравнений (количество уравнений и переменных в них) применим метод Крамера?

Метод Гаусса.

6.1. В чем суть метода Гаусса?

6.2. Что применяют для получения треугольной (ступенчатой) системы уравнений?

6.3. Для каких систем уравнений (количество уравнений и переменных в них) применим метод Гаусса?

Матричный метод.

7.1. В чем суть матричного метода?

7.2. Для каких систем уравнений (количество уравнений и переменных в них) применим матричный метод?

7.3. Матрицу какого вида используют для решения системы матричным методом?

7.4. Какое равенство используют для решения системы матричным методом?

ЗАДАНИЯ ДЛЯ САМОПРОВЕРКИ

Вариант I

1. Данная запись есть

а) Матрица размера mxn;

б) Определитель 3^го порядка;

в) Матрица 4^го порядка.

2. Если элементы двух строк матрицы пропорциональны, то ее определитель равен:

а) 1;

б) 0;

в) -1

3. Данная матрица есть

а) Диагональная;

б) Матрица-строка;

в) Нулевая.

4. Данные формулы есть формулы для решения систем уравнения по:

а) Методу Крамера;

б) Методу Гаусса;

в) Матричному методу.

5. Обратная матрица не существует, если:

а) ;

б) ;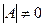

в) .

6. Матрица и 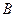можно сложить, если

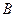а) - матрица строка, - матрица столбец;

б) и 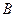одинокого размера;

в) - нулевая матрица размера , 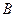- диагональная - порядка.

7. Возвести матрицу в степень

Ответ: а) ; б) ; в) .

8. Посчитать определитель по теореме Лапласа:

Ответ: а) 1; б) 0; в) 3.

9. Решить систему методом Гаусса:

а) ; ; ;

б) ; ; ;

в) ; ; .

10. Сформулировать теорему Лапласа и записать формулы разложения по элементам строки и столбца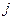

Вариант II

1. Данная запись есть

а) Определитель 3го порядка;

б) Матрица размера ;

в) Единичная матрица.

2. Если - матрица, транспонированная по отношению к матрице , то ее определитель

а) Равен 0;

б) Равен 1;

в) Равен .

3. Данная матрица есть

а) Матрица – столбец;

б) Нулевая;

в) Диагональная.

4. Данные формулы позволяют вычислить определитель:

а) 2го порядка;

б) по правилу Сарруса;

в) по теореме Лапласа.

5. Матрицу можно возвести в степень, если матрица

а) квадратная;

б) размера , ;

в) размера , .

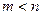6. Матрицу можно умножать на матрицу 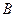, если:

г) число столбцов матрицы больше числа строк матрицы ;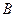

д) число столбцов матрицы А меньше числа строк матрицы В;

е) число столбцов матрицы А равно числу строк матрицы В.

7. Перемножить матрицы

и

Ответ: а) ; б) ; в) .

8. Посчитать определитель по правилу Сарруса:

Ответ: а)0; б) 4; в) 12.

9. Решить систему методом Крамера:

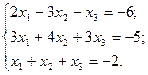
ж) ; ; ;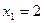

з) ; ; ;

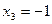и) ; ; .

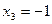10. Дать определение матрицы размера и записать ее в общем виде.

ЛИТЕРАТУРА

1.Высшая математика для экономистов - Учебник для вузов под ред. Н.Ш. Кремер и др., - Москва, ЮНИТИ, 2003.

2.Барковський В.В., Барковська Н.В. - Вища математика для економістів – Київ, ЦУЛ, 2002.