ПРИМЕР РЕШЕНИЯ СИСТЕМЫ ВСЕМИ ТРЕМЯ МЕТОДАМИ

Решить систему линейных алгебраических уравнений методами Крамера, Гаусса и матричным методом.

I. Метод Крамера.

Количество уравнений (3) равно количеству переменных (3), значит, матрица системы квадратная и имеет определитель.

Вычислим определитель матрицы системы:

- значит, система уравнений имеет единственное решение, которое находят по формулам Крамера: , .

Заменяем 1–й столбец столбцом свободных членов

Заменяем 2-й столбец столбцом свободных членов

Заменяем 3-й столбец столбцом свободных членов

Ответ: .

II. Матричный метод.

Данную систему уравнений можно записать в матричной форме :

, откуда .

Найдем матрицу, обратную матрицу . Так как , такая матрица существует. Найдем алгебраические дополнения к элементам матрицы по формуле :

; ; ;

; ; ;

; ; .

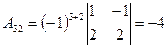Тогда

.

А теперь найдем решение системы:

.

Ответ: .

III. Метод Гаусса.

Выполним преобразования:

Сделаем коэффициенты при х равными нулю.

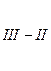Т.к. коэффициенты при z во II и III уравнениях системы равны, то можно из III уравнения вычесть II уравнение.

Таким образом, получили, что II уравнение системы есть уравнение с одной переменной, значит, можно вычислить значение переменной у.

Теперь последовательно, с помощью подстановки, вычисляем значения

переменных z и х.

Ответ: .