
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
УПРАЖНЕНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ. v Необходимые условия применения метода Крамера:
v Необходимые условия применения метода Крамера:
a. Количество уравнений системы должно равняться количеству неизвестных.
b. Определитель основной матрицы системы не должен равняться нулю:  .
.
Решение по правилу Крамера находят по формулам:
 , где
, где  , где
, где  ,
,
а  - определитель, который получается из основного определителя матрицы
- определитель, который получается из основного определителя матрицы  заменой
заменой  - го столбца столбцом свободных членов системы.
- го столбца столбцом свободных членов системы.
v При решении системы матричным способом сначала надо найти  . Система имеет решение при условии
. Система имеет решение при условии  . Затем ищут обратную матрицу к матрицу
. Затем ищут обратную матрицу к матрицу  :
:  . После этого умножают
. После этого умножают  на матрицу – столбец свободных членов системы:
на матрицу – столбец свободных членов системы: 
Полученная при этом матрица-столбец и является решением системы.
v Метод Гаусса состоит в приведении системы к треугольному виду. Для системы, состоящей из 3-х уравнений с 3-мя неизвестными метод Гаусса выглядит так: исключаем  из 2-го и 3-го уравнений системы: затем исключаем
из 2-го и 3-го уравнений системы: затем исключаем 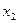 из 3-го уравнения и решаем полученную систему.
из 3-го уравнения и решаем полученную систему.
Решить каждую систему линейных алгебраических уравнений всеми тремя
способами:
1)  2)
2) 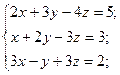 3)
3) 
4) 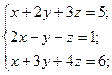 5)
5) 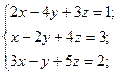 6)
6) 
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
Дата добавления: 2014-11-13; просмотров: 336; Мы поможем в написании вашей работы!; Нарушение авторских прав |