
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Определения: 1. Если определитель матрицы ≠ 0, то матрица называется невырожденной или неособенной.
Если определитель матрицы  =0, то матрица называется вырожденной или особенной.
=0, то матрица называется вырожденной или особенной.
2. Присоединенная матрица  , получается из матрицы
, получается из матрицы  , транспонированной по отношению к матрице
, транспонированной по отношению к матрице 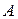 , заменой элементов матрицы
, заменой элементов матрицы  на их алгебраические дополнения.
на их алгебраические дополнения.
Теорема (необходимое и достаточное условие существования обратной матрицы):
Обратная матрица  существует и единственна тогда и только тогда, когда матрица
существует и единственна тогда и только тогда, когда матрица  невырожденная, т.е.
невырожденная, т.е.  . Ее элементы вычисляются по формуле:
. Ее элементы вычисляются по формуле:  .
.
Алгоритм построения обратной матрицы
1. Вычислим определитель данной матрицы  . Если . Если 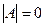 , то для
данной матрицы не существует обратной.
2. Если , то для
данной матрицы не существует обратной.
2. Если  , строим матрицу , строим матрицу 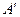 , транспонированную по отношению к матрице , транспонированную по отношению к матрице  , заменяя строки матрицы А ее столбцами.
3. Строим присоединенную матрицу , заменяя строки матрицы А ее столбцами.
3. Строим присоединенную матрицу  , заменяя элементы матрицы , заменяя элементы матрицы 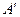 их алгебраическими дополнениями по формуле их алгебраическими дополнениями по формуле 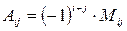 4. Вычисляем обратную матрицу по формуле
4. Вычисляем обратную матрицу по формуле 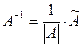 5. При необходимости проверяем правильность вычисления обратной матрицы
5. При необходимости проверяем правильность вычисления обратной матрицы  , исходя из ее определения , исходя из ее определения  . .
|
Пример:  . Найти . Найти 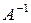 . .
|
1. 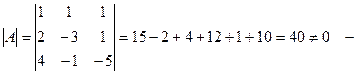 данная матрица имеет обратную. данная матрица имеет обратную.
|
2. 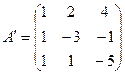 . .
|
3. 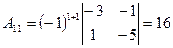 ; ; 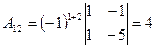 ; ;  ; ;
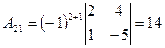 ; ;  ; ;  ; ;
 ; ; 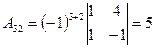 ; ;  .
Получили присоединенную матрицу: .
Получили присоединенную матрицу:
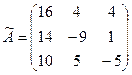 . .
|
4. 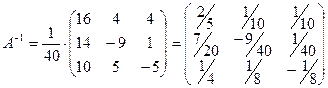 . .
|
Дата добавления: 2014-11-13; просмотров: 448; Мы поможем в написании вашей работы!; Нарушение авторских прав |