
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
УПРАЖНЕНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1) Правило нахождения определителей второго порядка можно записать в виде формулы:

Вычислить определители 2-го порядка матриц:
а)  ; б)
; б)  ; в)
; в) 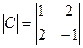 ; г)
; г)  .
.
2) Для вычисления определителей третьего порядка используют правило Сарруса или правило треугольников, которое проще запоминается в виде следующих схем:

 (+)
(главная диагональ)
(+)
(главная диагональ)
|

|  (-)
(другая диагональ)
(-)
(другая диагональ)
|
Вычислить определители 3-го порядка матриц по правилу Сарруса:
а) 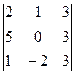 ; б)
; б) 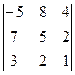 ; в)
; в) 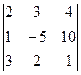 ;
;
3) Для вычисления определителей 4-го и более высокого порядка используют правило вычисления определителя методом разложения по элементам строки или столбца (по теореме Лапласа): определитель равен сумме произведений всех элементов какого-либо столбца (или строки) на соответствующие им алгебраические дополнения. Обычно вычисление проводится по элементам 1-й строки.
Можно использовать теорему Лапласа и для вычисления определителей 3-го порядка, когда разложение по первой строке имеет вид:

Вычислить определители 4-го и 3-го порядков:
а) 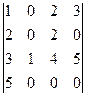 ; б)
; б) 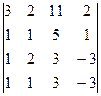 ; в)
; в)  ;
;
г)  ; д)
; д)  ; е)
; е) 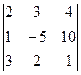 .
.
Замечание: Для сокращения вычислений удобно определитель раскладывать по элементам той строки или столбца, где содержится наибольшее количество нулей.
В этом случае нужно находить алгебраическое дополнения к элементам, равным 0; если же строки или столбцы не содержат достаточного количества нулей, то удобно провести эквивалентные преобразования. Используют правило: если ко всем элементам строки (столбца) прибавить соответствующие элементы другой строки (столбца); умноженные на одно и то же число; то определитель не изменяется.
III. «РАНГ МАТРИЦЫ»
Для решения и исследования некоторых математических и прикладных задач большое значение имеет понятие ранга матрицы.
Рассмотрим матрицу А размера .
.
В матрице А размера вычеркиванием каких-либо строк и столбцов можно вычленить квадратные подматрицы k-го порядка, где (меньшего из т и п). Определители таких подматриц называются минорами k-го порядка матрицы А. Один элемент матрицы называют минором первого порядка.
Из матрицы А размером 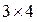 можно получить подматрицы 1-го, 2-го, 3-го порядков.
можно получить подматрицы 1-го, 2-го, 3-го порядков.
Пример: Выделим указанные подматрицы из данной матрицы  и запишем их миноры.
и запишем их миноры.
Решение:
Некоторые подматрицы первого порядка А  =
= 
некоторые подматрицы второго порядка А  =
= 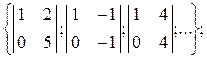
некоторые подматрицы третьего порядка А  =
= 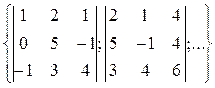 .
.
Дата добавления: 2014-11-13; просмотров: 523; Мы поможем в написании вашей работы!; Нарушение авторских прав |