КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
III. Операции над матрицами
1). Транспонирование матрицы -
- переход от матрицы 
к матрице 
, в которой строки и столбцы поменялись местами. Матрица называется транспонированной по отношению к матрице .
, 
.
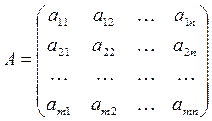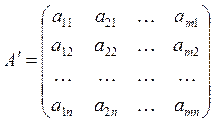Пример:
= 
; 
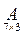2). Умножение матрицы на число.
Произведением матрицы 
на число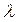 
называется матрица 
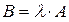, каждый элемент которой 
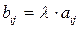для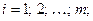 
.
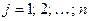Т.е., чтобы умножить матрицу на число, надо умножить на это число каждый элемент матрицы.
Пример:
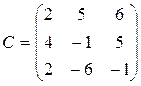, тогда
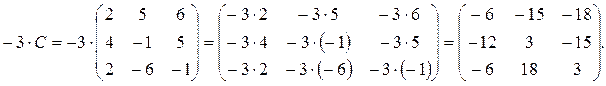
Следствие. Общий множитель всех элементов матрицы можно выносить за знак матрицы.
Пример: Вынести за знак матрицы общий множитель.
= 
.
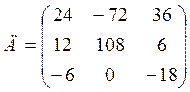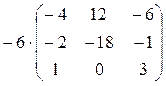Произведение матрицы на число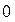 
есть нулевая матрица: 
.
3) Сложение матриц.
Суммой двух матрицА и В одинакового размера называетсяматрицаС=А+В, каждыйэлементкоторой 
Т.е., чтобы сложить две матрицы одинакового размера, надо сложить их соответствующие элементы.
Пример: 
4) Умножение матриц.
Умножение матрицы на матрицу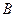 
определено, когда число столбцов матрицы равно число строк матриц 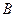, т.е. они согласованы.
Произведением матриц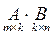 
называется такая матрица 
, каждый элемент которой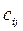 
равен сумме произведений элементов строки 
матрицы 
на соответствующие элементы столбца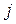 
матрицы 
.
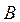Пример:
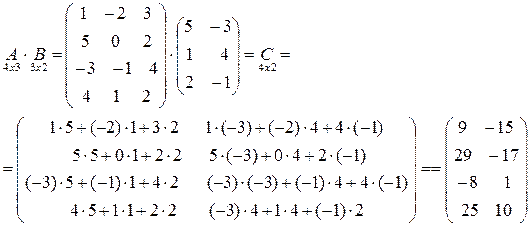
5) Возведение в степень.
Целой положительной степенью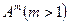 
квадратной матрицы называется произведение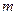 
матриц, равных , т.е.
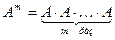. По определению полагают, 
.
Пример:
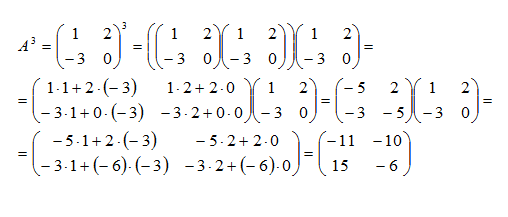
Дата добавления: 2014-11-13; просмотров: 297; Мы поможем в написании вашей работы!; Нарушение авторских прав |