Для упрощения вычисления определителей используют следующие свойства определителей.

1) Если какая-либо строка (столбец) матрицы состоит из одних нулей, то ее определитель равен 0.

Пример:

.

2) Если все элементы какой-либо строки (столбца) матрицы умножить на число , то и определитель матрицы умножится на это число .

Замечание. За знак определителя можно выносить общий множитель элементов любой строки или столбца.

Примеры: ;

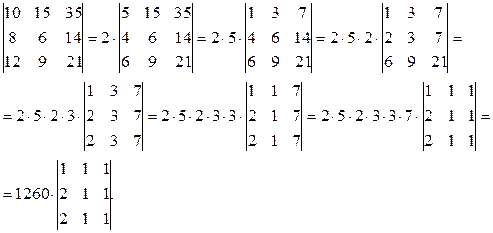
3) При транспонировании матрицы ее определитель не изменяется:

Пример:

; .

4) При перестановке двух строк (столбцов) матрицы ее определитель меняет свой знак на противоположный.

Пример:

; ; .

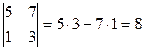5) Если квадратная матрица содержит две одинаковые строки (столбца), то ее определитель равен 0.

Пример:

.

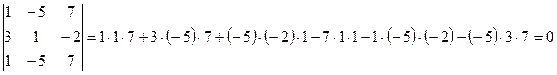6) Если элементы двух строк (столбцов) матрицы пропорциональны, то ее определитель равен 0.

Пример: Воспользуемся при вычислении свойствами 2) и 5) определителей:

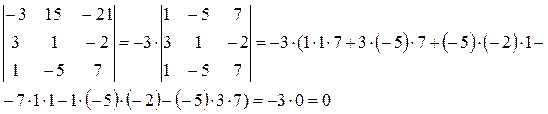
7) Сумма произведений элементов какой-либо строки (столбца) матрицы на алгебраические дополнения элементов другой строки (столбца) этой матрицы равна 0, т.е.

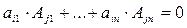при i j.

Пример: Посчитать: 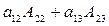= 0 для данной матрицы

.

=

.

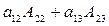8) Определитель матрицы не изменяется, если к элементам какой-либо строки (столбца) матрицы прибавить элементы другой строки (столбца), предварительно умноженные на одно и то же число.

Пример: Вычислить определитель матрицы С и матрицы С , полученной из матрицы С прибавлением ко второй строке матрицы С ее первой строки, умноженной на число -2:

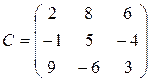
Воспользуемся уже полученным результатом определителя матрицы С:

Преобразуем матрицу С согласно свойству: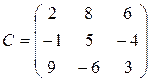

.

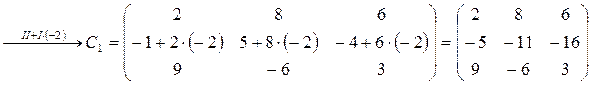Теперь вычислим определитель получившейся матрицы:

9) Сумма произведений произвольных чисел 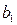, ,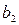…, 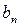на алгебраические дополнения элементов любой строки (столбца) равны определителю матрицы, полученной из данной заменой элементов этой строки (столбца) на числа

10) Определитель произведения двух квадратных матриц равен произведению их определителей:

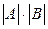, где А и В – матрицы n-го порядка.

Пример: вычислить с помощью свойств определителя определитель матрицы В четвертого порядка

.

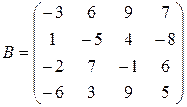Решение: