ОПРЕДЕЛЕНИЕ. Рангом матрицы А называется наивысший порядок отличных от нуля миноров этой матрицы.

Обозначение: rang A или r(A)

Из определения следует:

1) т.е., не превосходит меньшего из ее размеров;

2) тогда и только тогда, когда все элементы матрицы равны нулю;

3) для квадратной матрицы п-го порядка тогда и только тогда, когда матрица А – невырожденная, т.е., ее определитель не равен нулю.

Пример: Вычислить , если

.

Решение: Начнем с перебора миноров третьего порядка.

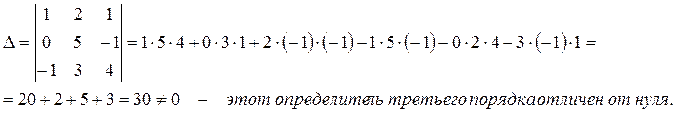Таким образом, согласно определения ранга матрицы, можем сделать вывод, что ранг данной матрицы равен 3, т.е., .

Замечание: В данном случае вычисление уже первого минора третьего порядка привело к искомому результату. В общем же случае определение ранга матрицы перебором миноров всех возможных порядков достаточно трудоемко.

Для упрощения решения этой задачи используются элементарные преобразования, сохраняющие ранг матрицы:

1)отбрасывание нулевой строки (столбца) матрицы;

2)умножение всех элементов строки (столбца) матрицы на число, не равное нулю;

3)изменение порядка строк (столбцов) матрицы;

4)прибавление к каждому элементу одной строки (столбца) матрицы соответствующих элементов другой строки (столбца), умноженных на одно и то же число;

5)транспонирование матрицы.