
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Метод Крамера».
Теорема Крамера: Пусть определитель матрицы 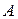 системы D, а
системы D, а  j– определители матриц, получаемых из данных заменой j-го столбца на столбец свободных членов. Тогда, если
j– определители матриц, получаемых из данных заменой j-го столбца на столбец свободных членов. Тогда, если 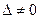 , то система имеет единственное решение, которое вычисляется по формулам КРАМЕРА:
, то система имеет единственное решение, которое вычисляется по формулам КРАМЕРА:  , где j=1; …;
, где j=1; …; 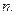
| Алгоритм метода Крамера | Пример. Решить систему уравнений методом Крамера: 
| |
1. Записать матрицу  системы и найти ее определитель D, если D = 0 , то система решений не имеет. системы и найти ее определитель D, если D = 0 , то система решений не имеет.
| 1.  система имеет единственное решение. система имеет единственное решение.
| |
2. Если 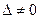 , то находим , то находим  j, заменяя j-й столбец столбцом свободных членов. j, заменяя j-й столбец столбцом свободных членов.
| 2. 

| |
3. По формулам Крамера находим х  : :

|  Ответ: Ответ: 
| |
2.«Матричный метод».
Если определитель матрицы  системы
системы 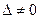 , то матрица системы невырожденная, а значит, имеет обратную матрицу
, то матрица системы невырожденная, а значит, имеет обратную матрицу  . Умножим обе части матричного равенства
. Умножим обе части матричного равенства  на обратную матрицу
на обратную матрицу  слева, получим равенство:
слева, получим равенство:  , или
, или  , откуда
, откуда 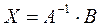 - равенство, выражающее суть матричного метода.
- равенство, выражающее суть матричного метода.
| Алгоритм матричного метода | Пример:
Решить систему матричным методом.

|
| 1. Записать матрицу системы и найти ее определитель. Если определитель равен нулю, то система не имеет решений. |  -система имеет решение, матрица системы имеет обратную. -система имеет решение, матрица системы имеет обратную.
|
2. Ищем матрицу  , обратную матрице , обратную матрице  системы по формуле системы по формуле 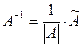 , где , где  связана с связана с 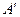 (нужно транспонировать матрицу (нужно транспонировать матрицу  ). ).
|  ; ;  Заменяем элементы транспонированной матрицы
Заменяем элементы транспонированной матрицы 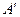 их алгебраическими дополнениями: их алгебраическими дополнениями:
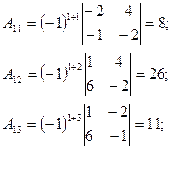 
 Теперь запишем
Теперь запишем  , и так и оставляем (для удобства последующих вычислений). , и так и оставляем (для удобства последующих вычислений).
|
3. Ищем матрицу – столбец  значений переменных системы по формуле значений переменных системы по формуле 
|  Ответ: Ответ:  . .
|
Дата добавления: 2014-11-13; просмотров: 333; Мы поможем в написании вашей работы!; Нарушение авторских прав |