Свойства определителей.

2.1. Что можно сказать об определителе матрицы, у которой:

2.1.1 одна строка содержит только нулевые элементы;

2.1.2 элементы двух столбцов равны;

2.1.3 элементы двух строк пропорциональны;

2.1.4 две строки матрицы поменяли местами;

2.1.5 к элементам одного столба прибавили соответствующие элементы другого столбца, умноженные на одно и то же число.

2.2. Сравните определители матрицы и матрицы 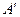, транспонированной по отношению к матрице .

2.3. Как вычисляют определители квадратных матриц:

2.3.1 второго порядка;

2.3.2 третьего порядка;

2.3.3 четвертого порядка

2.4. Чем матрица отличается от определителя матрицы?

Ранг матрицы.

3.1. Что такое ранг матрицы?

3.2. Как проще вычислить ранг матрицы? Какие элементарные преобразования матриц при этом применяются?