
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Метод Гаусса».
Или метод последовательного исключения переменных - заключается в том, что с помощью элементарных преобразований данная система уравнений приводится к равносильной системе уравнений ступенчатого (треугольного) вида, из которой, последовательно, начиная с последней переменной, находятся все остальные переменные.
Системой треугольного (ступенчатого) вида называется система вида

Получают такую систему с помощью следующих элементарных преобразований систем линейных неоднородных алгебраических уравнений:
1. изменение порядка уравнений системы,
2. умножение или деление обеих частей любого уравнения системы на одно и то же не равное нулю число,
3. почленное сложение уравнений системы.
Пример. Решить данную систему методом Гаусса.

| Пояснения по ходу решения. |

| Сделаем III-е уравнение системы I-м. |
 
| Сделаем коэффициенты при х1 равными нулю с помощью элементарных преобразований 2. и 3. |
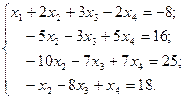
| Сделаем IV-е уравнение системы II -м. |
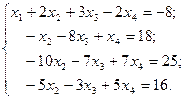 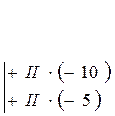
| Сделаем коэффициенты при х  равными нулю с помощью элементарных преобразований 2. и 3.
равными нулю с помощью элементарных преобразований 2. и 3.
|
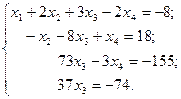
| Получили IV-е уравнение как уравнение с одной переменной, решая его, найдем значение переменной х 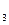
|
 Ответ:
Ответ: 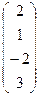 . .
| Из последнего уравнения, подставляя найденное значение переменной х 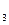 , находим значение переменной х4 , подставляем его во II уравнение и находим из этого уравнения значение переменной х , находим значение переменной х4 , подставляем его во II уравнение и находим из этого уравнения значение переменной х  , затем с помощью подстановки в уравнение I находим значение переменной х1.Записываем ответ. , затем с помощью подстановки в уравнение I находим значение переменной х1.Записываем ответ.
|
Дата добавления: 2014-11-13; просмотров: 378; Мы поможем в написании вашей работы!; Нарушение авторских прав |