II. Виды матриц

1.Две матрицы и 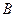одного размера называются равными, если они совпадают поэлементно, т.е. для любых .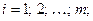

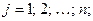2. 3. Матрица, состоящая из одной строки, называется матрицей– строкой, а из одного столбца – матрицей -столбцом:

- матрица-строка; = .
- матрица-столбец, .

o Матрица называется квадратной -го порядка, если число ее строк равно числу столбцов и равно .
Пример:

- квадратная матрица 3^го порядка

Элементы матрицы , у которых номер столбца равен номеру строки 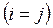, называются диагональными и образуют главную диагональ матрицы.

Для квадратной матрицы главную диагональ образуют элементы .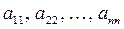

o Если все недиагональные элементы квадратной матрицы равны нулю, то матрицы называется диагональной.

Пример:

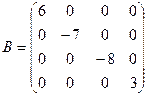- диагональная матрица 4-го порядка

o Если у диагональной матрицы -го порядка все диагональные элементы равны единице, то матрица называется единичной матрицей -го порядка и обозначается .

Пример:

- единичная матрица третьего порядка.