
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Оценка риска с учетом получения выигрыша или возможных потерь
Риск – это возможность неблагоприятного исхода. Величина риска – вероятность наступления случая потерь, а также размер возможного ущерба от него.
Вероятность любого события колеблется от 0 – 1.
Вероятность наступления случая потерь и получения возможного ущерба.

Следовательно, для оценки риска можно использовать следующие выражения R = Hn × Pn.
Таким образом степень риска определяется как произведение ожидаемого ущерба на вероятность того, что такой ущерб будет нанесен. На практике принято рассматривать коэффициент (P) = (r); определяется как отношение возможных максимальных потерь (Hn max) и V собственных финансовых ресурсов.

Величина r определяет риск банкротства.
В большинстве случаев указанные коллективные оценки риска и методы их определения используются для оценки отдельных видов риска. Вместе с тем они могут быть использованы и для оценки риска проекта ценам. Это к случаям, когда имеются коллективные данные по каждому риску или когда для оценки риска проекта используются экспертные методы, в процессе которых оценивается вероятность успешной реализации проекта и/или величина возможных потерь вследствие наступления различного рода нежелательных исходов.
Таким образом, коэффициент риска (Р) рассчитывается как:
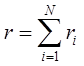
Н – число учитываемых видов риска;
R – обобщенный коэффициент (Р) процента;
N – число учитываемых видов (Р).

После определения риска в цифровом выражении он должен быть оценен как приемлемый, допустимый, критичный, катастрофичный.
Приемлемый минимальный(0,25) – характеризует уровень потерь и превышающий размеры чистой прибыли.
Допустимый (повышенный) (0,25-0,5) – характеризует уровень потерь не превышающего размеры расчетной прибыли.
Критический (0,5-0,75) характеризуется тем, что в границах этой зоны возможны потери, величина их превышает размеры расчетной прибыли, но не превышает размер ожидаемых доходов.
Зона критического риска характеризуется опасностью потерять не только прибыль, но и средства, вложенные предпринимателем в операцию.
Катастрофичный (недопустимый) ( 0,75) – характеризуется тем, что в пределах этой зоны ожидаемые потери способны привести размер ожидаемых дивидендов от операции и достичь величины равной всему имущественному состоянию предпринимателя.
Реально означает, что предприниматель теряет не только средства, вложенные в операцию, но и многое сверх того, вплоть до полного банкротства.
Рассмотренные шкалы риска приемлемы как для оценки приемлемости уровня отдельных рисков, так и для риска проекта в целом.
Задача. Требуется определить величину риска вложения средств по каждому из 2х вариантов и выбрать наиболее приемлемый из них исходя из следующих данных:
- возможный ущерб в случае отсутствия сбыта продукции
а) по 1му варианту 10 млн. руб
б) по 2му варианту 5 млн.руб
- вероятность реализации проекта вложения средств: а) 0,75 б) 0,95
Решение :
а) Рп = 1 – Рв = 1- 0,75 = 0,25 б) Рп = 1-0,95 = 0,05
Rа = Нп * Рп = 10*0,25 = 2,5 Rб = 0,05*5 = 0,2
Задача. Определить величины риска изучения и риска действия, а также совокупную величину риска инвестирования средств в одном из 2х регионов, выбрав при этом наиболее приемлемый при следующих данных:
С1, С2 предполагаемая стоимость строительства соответственно в 1 и 2 регионах (млрд.руб)
С1 = 30, С2 = 27
Р11, Р12 вероятность наступления стихийных бедствий особенно в 1 и 2 регионах.
Р11 = 0,2, Р12 = 0,22
Р21, Р22 вероятность перепрофилирования
Р21 = 0,10, Р22 = 0,08
У1, У2 предполагаемая степень ущерба в случае наступления стихийных бедствий %
У1 = 90, У2 = 95
Д1, Д2 доля затрат на перепрофилирование по отношению к предполагаемой стоимости строительства %
Д1 = 70, Д2 = 90
Решение :
Риск изучения – потери, вызванные недостаточность модели пр-ем.
Ризуч = Д * С * Р изуч.
Д – уд. Вес С – предполагаемая стоимость изучения.
Риск действия – потери, вызванные недостаточностью управления пр-ем.
Rg = У * С * Pg, где У – предполагаемая степень ущерба
Rg – вероятность наступления стихийных бедствий.
Р1изуч = 70*30*0,10 = 210 млрд.руб
Р2изуч = 90*27*0,23 = 589,95 млрд.руб
R1g = 90*30*0.2 = 540 млрд.руб
R2g = 95*27*0.23 = 589.95 млрд.руб
Сов риск1 = 210+540 = 750 млрд.руб
Сов риск2 = 589,95+194,4 = 784,35 млрдюруб
2.13. Сравнительная оценка вариантов решений с учетом риска
На практике для сравнительной характеристики проектов по степени риска особенно в инвестиционо-финансовой сфере в качестве количественного критерия используется ср.ожидаемое значение результата и средне квадратичное отклонение, как мера изменчивости возможного результата.
Задача: Например имеется 2 варианта пр-ва новых товаров. С учетом неопределенности ситуаций были проанализированы возможные доходы от реализации проектов. Исходные данные:
| Характеристика ситуации | Возможный доход | Вероятность наступления |
| Проект А | ||
| 1. пессимистический | 0,2 | |
| 2. наиболее вероятный | 0,6 | |
| 3. оптимистический | 0,2 | |
| Проект В | ||
| 1. пессимистический | 0,25 | |
| 2. наиболее вероятный | 0,5 | |
| 3. пессимистический | 0,25 |
Пессимистическая ситуация : А 100(0,2) ≥≠В80 (0,2)
Наиболее вероятная : А333(0,6) δa ≤≠ δb В 300(0,5)
Оптимистическая ситуация : А500(0,2) ≤≠В 600(0,25)
E = ∑Pi * Xi
Ea = 100*0.2+333*0.6+500*0.2 = 319.8
Eb = 80*0.25+300*0.5+600*0.25 = 320
D = (Xi – E)2 * Pi
Da = (100-319.8)2 * 0.2+(333-319.8)*0.6+(500-319.8)*0.2 = 16261.36
δ = √D
δa = 127.52 δb = 185
При сравнении сред. Доходности Ea и Eb. При сравнении возможного результата , получается
δa ≤≠ δb , следовательно вариант А более предпочтителен.
Предпочтение варианту А может быть отдано в следующих ситуациях:
δa ≤≠ δb, Еа = Ев,
δa = δb, Еа ≥≠ Ев
δa ≤≠ δb, Еа ≥≠ Ев.
Предпочтение проекту В:
δa ≥≠ δb, Еа = Ев
δa = δb, Еа ≤≠ Ев
2.14. Принятие решений в условиях риска
m – количество возможных решений
Р1,2,3 – решение
n – количество предположений
О – предположение при неизвестных условиях установки
а – результат (выигрыш) соответствующей каждой паре состояний решений Р и постановки О.
Эффективность принятия решения можно представить в виде таблицы:
| Варианты решений | Варианты условий обстановки | |||
| О1 | О2 | … | Оn | |
| P1 | 
| 
| … | 
|
| P2 | 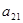
| 
| … | 
|
| … | … | … | … | … |
| Pm | 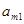
| 
| … | 
|
Выбор решения в условиях риска предполагает, что вероятности возможных вариантов обстановки известны. Эти вероятности определяются на основе статистических данных или экспертных оценок. Наличие выигрышей являющиеся показателями различных решений при различных условиях обстановки позволяет определить потери в результате принятия неоптимистических решений – в случае, когда ожидаемое условие обстановки не произошло.
При выборе решения в качестве критерия риска используется Р=Нр.
Например: предприятие готовится к переходу на новые виды продукции, при этом возможны 4 варианта решений Р1,Р2,Р3,Р4. Каждому из вариантов соответствует определенный вид выпуска или их сочетание. Варианты обстановки О характеризует структуру спроса на новую продукцию, которые могут быть трех видов О1,О2,О3.
«Расчет выигрыша»
Таблица1
| Варианты решений | Варианты условий обстановки | ||
| О1 | О2 | О3 | |
| Р1 | 0,25 | 0,35 | 0,4 |
| Р2 | 0,75 | 0,2 | 0,3 |
| Р3 | 0,35 | 0,82 | 0,1 |
| Р4 | 0,8 | 0,2 | 0,35 |
Если поступит обстановка О1,то необходимо принять решение Р4, если обстановка О2, то Р3; если О3, то Р1.
Если пре6дприятие принимает решение Р3 в надежде на обстановку О2, а наступает обстановка О1,то предприятие получает выигрыш 0,35 вместо 0,82. Тогда потери при принятии решения Р3 и наступления обстановки О1 составит 0,8-0,35 = 0,45. следовательно, в общем случае потери, соответствующие каждой паре сочетаний решений Р и обстановки О определяется, как разность между выигрышем и выигрышем по конкретному решению при данной обстановке.
Определим возможные потери при различных обстановках:
«Расчет потерь»
Таблица2
| Варианты решений | Варианты условий обстановки | ||
| О1 | О2 | О3 | |
| Р1 | 0,55 | 0,47 | |
| Р2 | 0,05 | 0,62 | 0,1 |
| Р3 | 0,45 | 0,3 | |
| Р4 | 0,62 | 0,05 |
При расчете условной вероятности обстановки принимаем следующие значения РО1=0,5; РО2=0,3; РО3=0,2.
Р1=0,55*0,5+0,47*0,3+0,02*0=0,416
Р2=0,05*0,6+0,62*0,3+0,1*0,2=0,231
Р3=0,045*0,5+0*03+0,3*0,2=0,285
Р4=0*0,5+0,52*0,3+0,05*0,2=0,196
Решение Р4 является наиболее безопасным.
Принятие решений в условиях неопределенности производиться на основе выбора критериев, к которым относятся:
- принцип недостаточного обоснования Лапласа
- максимальный критерий Вальда
- минимальный критерий Севиджа
- критерий обобщенного максимина –Гурвица (пессимизма, оптимизма)
Принцип недостаточного обоснования Лапласа используется в случае, если можно предположить, что любой из вариантов обстановки не долее вероятен, чем другой, тогда вероятности обстановки могут считать равными и производить выбор решения также, как и в условиях риска, то есть по минимуму средневзвешенному показателю риска.
При учете трех вариантов обстановки вероятность варианта составляет 0,33.
Р1=0,55*0,33+0,47*0,33+0*0,33=0,3366
Р2=0,05*0,33+0,62*0,33+0,1*0,33=0,2541
Р3=0,45*0,33+0*0,33+0,3*0,33=0,2475
Р4=0*0,33+0,82*0,33+0,05*0,33=0,2111
Предпочтение отдается решению Р4=0,2111
Максимальный критерий Вальда используется в случаях, когда требуется гарантия, чтобы выигрыш в любых условиях оказывался не менее, чем наибольшим из возможных худших условиях. наилучшим решением считается то, для которого выигрыш окажется максимальным из всех минимальных при всех вариантах условий. Критерий, используемый при таком подходе получил название максимина, то есть в качестве исходных данных при выборе является выигрыш  соответствующий которой паре сочетаний решений при обстановке О. Данный критерий выбирается на основе таблицы.
соответствующий которой паре сочетаний решений при обстановке О. Данный критерий выбирается на основе таблицы.
При каждой обстановке выбирается наиболее эффективное решение О1Р1=0,25; О2Р2Р4=0,2; О3Р3=0,1
Следовательно, максимальным результатом выигрышем, который может быть получен в условиях имеющихся исходных данных является решение Р1 при обстановке О1.
Данный критерий ориентирует принимающего решение на слишком осторожную линию поведения.
Минимальный критерий Севиджа. Данный критерий используется в случаях, когда требуется в любых условиях избежать большого риска, в соответствии с этим критерием предпочтение отдается решению, для которого потери максимальные при различных вариантах окажутся минимальными. 
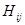 -потери
-потери
данный критерий определяется по таблице2.
Max – О1Р1Р3=0,55; 0,45; О2Р1Р2Р3
Min потери из возможных максимальных образуется при условиях обстановки О1 и при принятии решения Р3.
Критерий обобщенного максимина –Гурвица (пессимизма, оптимизма) используется, если требуется остановиться между линией поведения в расчете на лучшее. В этом случае предпочтение отдается варианту решений для которого окажется максимальным показатель G, определяемый по формуле:

k- коэффициент, рассматриваемый, как показатель оптимизма
при k=0, где линия поведения в расчете на лучшее
при k=0, где линия поведения в расчете на худшее
Например: к=0; 0,25; 0,5; 0,75; 1.
Таблица3
| Варианты решений | R | ||||
| 0,25 | 0,5 | 0,75 | |||
| Р1 | 0,4 | 0,3625 | 0,325 | 0,2875 | 0,25 |
| Р2 | 0,75 | 0,6125 | 0,475 | 0,3375 | 0,2 |
| Р3 | 0,82 | 0,64 | 0,46 | 0,28 | 0,1 |
| Р4 | 0,8 | 0,65 | 0,5 | 0,35 | 0,2 |
При к=0
G1=0*0,25+(1-0)*0,4=0,4
G2=0*0,2+(1-0)*0,75=0,75
G3=0*0,1+(1-0)*0,82=0,82
G4=0*0,2+(1-0)*0,82=0,8
При к=0,25
G1=0,25*0,25+(1-0,25)*0,4=0,0625+0,3=0,3625
G2=0,25*0,2+(1-0,25)*0,75=0,05+0,5625=0,6125
G3=0,25*0,1+(1-0,25)*0,82=0,025+0,615=0,64
G4=0,25*0,2+(1-0,25)*0,8=0,05+0,6=0,65
При к=0,5
G1=0,5*0,25+(1-0,5)*0,4=0,125+0,2=0,325
G2=0,5*0,2+(1-0,5)*0,75=0,1+0,375=0,475
G3=0,5*0,1+(1-0,5)*0,82=0,05+0,41=0,46
G4=0,5*0,2+(1-0,5)*0,8=0,1+0,4=0,5
При к=0,75
G1=0,75*0,25+(1-0,75)*0,4=0,1875+0,1=0,2875
G2=0,75*0,2+(1-0,75)*0,75=0,15+0,1875=0,3375
G3=0,75*0,1+(1-0,75)*0,82=0,075+0,205=0,28
G4=0,75*0,2+(1-0,75)*0,8=0,15+0,2=0,35
При к=1
G1=1*0,25+(1-1)*0,4=0,25
G2=1*0,2+(1-1)*0,75=0,2
G3=1*0,1+(1-1)*0,82=0,1
G4=1*0,2+(1-1)*0,8=0,2
В этом случае предпочтение отдается варианту решения Р4 у которого максимальный показатель G.
Вывод:В данной задаче самыми приемлемыми решениями являются Р4, так как при использовании данных решений минимальны потери и максимален выигрыш.
Дата добавления: 2014-12-03; просмотров: 387; Мы поможем в написании вашей работы!; Нарушение авторских прав |