
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
СТОИМОСТЬ ЗЕМЛИ С УЧЕТОМ РЕВЕРСИИ
Следуя (3.9) запишем стоимость земли 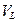 на период q=1.
на период q=1.
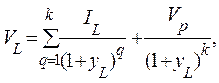 (3.10)
(3.10)

где 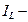 ежегодный чистый операционный доход с земельного участка,
ежегодный чистый операционный доход с земельного участка, 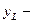 ставка процента на капитал, вкладываемый в землю. Ежегодный чистый операционный доход примем постоянным.
ставка процента на капитал, вкладываемый в землю. Ежегодный чистый операционный доход примем постоянным.
Для удобства дальнейших выводов вместо (3.10) возьмем выражение (3.5). Полагая величину Iq постоянной для каждого года и равной IL найдем
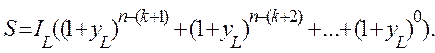
Выражение в скобках является суммой n-k членов геометрической прогрессии со знаменателем (1+y) и первым членом, равным 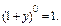 Тогда
Тогда

и соответственно
 (3.11)
(3.11)
Сравнивая (3.11) с (3.10) приравняем их вторые составляющие так
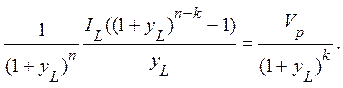 (3.12)
(3.12)
Разделив и умножив стоящее слева выражение на 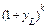 запишем
запишем
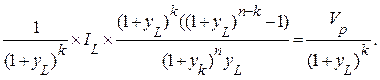
Очевидно, что
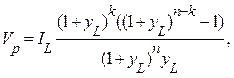
или

Поскольку земля есть неистощаемый источник доходов, то n стремится к бесконечности. При этом выражения 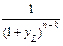 стремится к нулю и окончательно будет
стремится к нулю и окончательно будет
 (3.13)
(3.13)
Следовательно, денежный поток от реверсии земли равен капитализированному чистому операционному доходу. Тогда стоимость земли будет
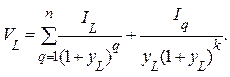 (3.14)
(3.14)
Это окончательная формула оценки стоимости земли по ежегодному чистому доходу. В частном случае при постоянном IL для каждого года в первом слагаемом оно будет суммой k членов геометрической прогрессии со знаменателем  и ее первым членом равным
и ее первым членом равным 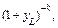
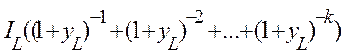
или

Тогда будет

После простых преобразований запишем
 (3.15)
(3.15)
При постоянном чистом операционном доходе стоимость земли равна его капитализированному значению.
Дата добавления: 2014-12-03; просмотров: 401; Мы поможем в написании вашей работы!; Нарушение авторских прав |