
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ МЕТОДА
Пусть имеют место факторы  влияющие на стоимость объекта
влияющие на стоимость объекта  Запишем в общем виде эту зависимость так
Запишем в общем виде эту зависимость так
 (7.1)
(7.1)
Если имеется некоторый сравниваемый объект с ценой 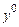 и значениями факторов
и значениями факторов 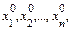 то вводя обозначения
то вводя обозначения
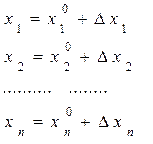 (7.2)
(7.2)
выражение (7.1) можно переписать так
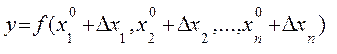 (7.3)
(7.3)
Разложение (7.2) в ряд Тейлора приводит к выражению
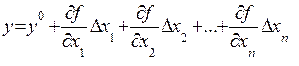 (7.4)
(7.4)
где  а
а 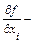 частная производная функции (7.1) по переменной
частная производная функции (7.1) по переменной 
В дальнейшем будут использоваться обозначения, приведенные в [2]. С их учетом выражение (7.4) перепишем так
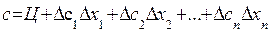 (7.5)
(7.5)
где 
Величина  называется вкладом в стоимость единицы j-го ценообразующего фактора.
называется вкладом в стоимость единицы j-го ценообразующего фактора.
В выражении (7.5) значения 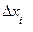 исходя из (7.2) можно найти так
исходя из (7.2) можно найти так
 ,
,
то есть это есть разность значений факторов оцениваемого объекта и сравниваемого. Значение  также известно – это стоимость сравниваемого объекта. Неизвестными являются величины:
также известно – это стоимость сравниваемого объекта. Неизвестными являются величины: 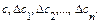 Всего n+1 величин. Для их определения необходимо составить систему k=n+1 уравнений вида
Всего n+1 величин. Для их определения необходимо составить систему k=n+1 уравнений вида
 (7.6)
(7.6)
Систему (7.6) можно переписать так
 (7.7)
(7.7)
В матричном виде (7.7) будет такой
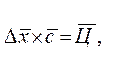 (7.8)
(7.8)
где
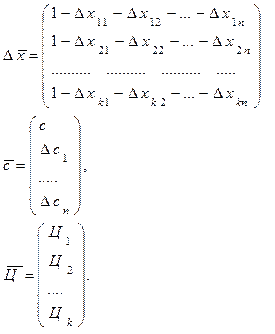
Из (7.8) можно найти
 (7.9)
(7.9)
где  обратная к
обратная к  матрица. Решение (7.9) является общим при числе уравнений
матрица. Решение (7.9) является общим при числе уравнений

Пример 7.1.Осуществить оценку стоимости объекта недвижимости площадью 250 м2 с гаражом без сада.
Решение:Для сравнения выбрано n+1=4 объекта, так как сравнение производится по числу факторов n, равном трем: площади, наличию гаража и наличию сада.
Сравниваемые объекты и объект оцени приведены в таблице 7.1.
Таблица 7.1.
Таблица сравнения
| Факторы | Объекты | |||||
| Оцениваемый | ||||||
| Площадь, м2 Гараж сад | х1 х2 х3 | есть есть | есть нет | есть есть | нет нет | есть нет |
| Цена, у.е. | Ц |
Цены участков приведены в условных единицах.
Значению «есть» положим в соответствие 1, а значению «нет» – 0. Тогда получим

В данном примере система уравнений имеет следующий вид

Ее решение методом Жордана приведено в таблицах 7.2 –7.6. В них 
Таблица 7.2
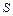
| 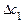
| 
| 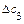
| |
| Ц1 Ц2 Ц3 Ц4 | -100 -100 -50 -50 | -1 |
Таблица 7.3
| Ц1 | 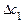
| 
| 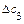
| |
| S Ц2 Ц3 Ц4 | +1 -1 -1 -1 | -100 +50 +50 | -1 | +1 -1 -1 |
Таблица 7.4
| Ц1 | Ц3 | 
| 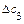
| |
S
Ц2
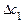 Ц4
Ц4
| -1 -1 -0,02 | +2 +0,02 -1 | -1 | +1 -1 -1 |
Таблица 7.5
| Ц1 | Ц3 | 
| Ц4 | |
S
Ц2
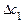
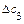
| -1 -1 -0,02 | +1 +1 +0,02 +1 | -1 +1 +1 | +1 -1 -1 |
Таблица 7.6
| Ц1 | Ц3 | Ц2 | Ц4 | |
S

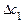
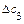
| -2 -1 -0,02 +1 | +2 +1 +0,02 | +1 +1 -1 | -1 |
Из последней таблицы найдем
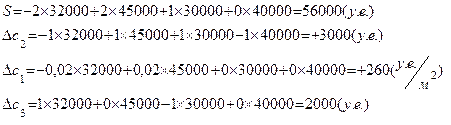
Контроль решения осуществляется подстановкой результата в исходную систему уравнений.
Дата добавления: 2014-12-03; просмотров: 313; Мы поможем в написании вашей работы!; Нарушение авторских прав |