Задача №1. Конус с углом при вершине и радиусом основания катится по неподвижной горизонтальной плоскости без скольжения

Конус с углом при вершине и радиусом основания катится по неподвижной горизонтальной плоскости без скольжения. Скорость центра основания постоянна.

Определить:

1. угловую скорость конуса ;

2. угловое ускорение конуса ;

3. скорости наинизшей и наивысшей точек основания А и В ;

4. ускорение этих точек .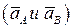

Решение:

1) Определяем угловую скорость конуса. ОР - мгновенная ось вращения.

2) Определяем угловое ускорение тела.

Для определения углового ускорения необходимо построить годограф угловой скорости . Вектор геометрически равен скорости конца вектора . В данном случае скорость является вращательной вокруг оси OZ. Угловая скорость этого вращения определяется как угловая скорость вращения оси ОС вокруг оси OZ.

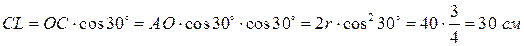
Скорость находим как вращательную скорость вектора угловой скорости - при вращении вокруг оси OZ.

т.е.

3) Определим скорости точек тела:

, т.к. точка А лежит на мгновенной оси вращения

4) Определяем ускорения точек тела.

Ускорение точки тела определяем как геометрическую сумму осестремительного ускорения во вращении тела вокруг мгновенной оси ОР и вращательного относительно оси углового ускорения .

Для определения вращательного ускорения опускаем из точки В перпендикуляр на ось углового ускорения, который совпадает с отрезком

в плоскости POZ

В точке А, лежащей на мгновенной оси вращения, осестремительное ускорение равно нулю:

Определяем модуль вращательного ускорения точки А: