
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Пример. Кривошипно-шатунный механизм
Угловая скорость кривошипа равна ωОА.Определить угловую скорость шатуна и скорости точек А,В, и С для трех положений механизма.
 Кривошип ОА вращается вокруг точки О, шатун АВ совершает плоское движение в плоскости чертежа. Во всех случаях скорость точки А перпендикулярна кривошипу и равна
Кривошип ОА вращается вокруг точки О, шатун АВ совершает плоское движение в плоскости чертежа. Во всех случаях скорость точки А перпендикулярна кривошипу и равна  , а скорость точки В направлена по горизонтальной прямой.
, а скорость точки В направлена по горизонтальной прямой.
1. Кривошип ОА образует острый угол с горизонтальной прямой (рис.18). В этом случае мгновенный центр скоростей шатуна находится в точке Р, где пересекаются восстановленные в точках А и В перпендикуляры к скоростям в этих точках.

Скорость точки С направлена перпендикулярно отрезку РС и находится из пропорции:
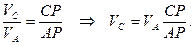
Угловая скорость шатуна равна 
Кривошип и шатун расположены на одной прямой (рис.19).
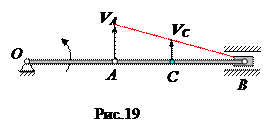 В этом положении мгновенный центр скоростей находится в точке В, поэтому скорость VB равна нулю. Скорость точки С находится из пропорции:
В этом положении мгновенный центр скоростей находится в точке В, поэтому скорость VB равна нулю. Скорость точки С находится из пропорции:
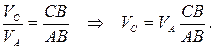
 Угловая скорость шатуна равна
Угловая скорость шатуна равна 
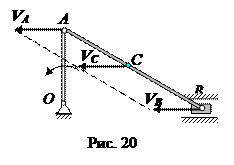
3. Кривошип занимает вертикальное положение (рис.20). В этом случае мгновенный центр скоростей шатуна находится в бесконечности, скорости всех его точек равны, угловая скорость шатуна равна нулю.
Пример1
 Известны радиусы
Известны радиусы 
 шестерей и угловая скорость
шестерей и угловая скорость
криволинейна AB 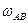 ,
,
Найти угловую скорость 3
Колеса 

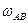

Найти скорость K, как точки сцепления 2 и 3.
Для шестерни 2:

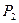 - мгновенный центр скоростей шестерен
- мгновенный центр скоростей шестерен
2 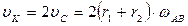
Тогда, 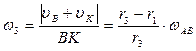
Когда, 
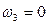
Дата добавления: 2014-12-03; просмотров: 513; Мы поможем в написании вашей работы!; Нарушение авторских прав |