КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Определение скоростей точек плоской фигуры
Зависимость между скоростями двух точек плоской фигуры.
Рассмотрим две точки А и В плоской фигуры. Положение точки В относительно неподвижной системы координат Оху определяется радиусом-вектором rB (рис.5):
rB = rA + ρ,
где rA - радиус-вектор точки А, ρ = АВ
вектор, определяющий положение точки В
относительно подвижных осей Ах1у1, перемещающихся поступательно вместе с полюсом А параллельно неподвижным осям Оху.
Тогда скорость точки В будет равна
.
В полученном равенстве величина 
является скоростью полюса А.
Величина 
равна скорости, которую точка В получает при 
= соnst, т.е. относительно осей Ах1у1 при вращении фигуры вокруг полюса А. Введем для этой скорости обозначение 
:
.
Следовательно, 
|
. (2)
Скорость вращательного движения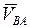 
точки направлена перпендикулярно отрезку АВ и равна
Модуль и направление скорости точки В находится построением соответствующего параллелограмма (рис.6).
Пример 1. Найти скорости точек А, В и D обода колеса, катящегося по прямолинейному рельсу без скольжения, если скорость центра колеса С равна VC.
Решение. Выбираем точку С, скорость которой известна за полюс. Тогда скорость точки А равна
,
где 
и по модулю 
.
Значение угловой скорости ω найдем из условия того, что точка Р колеса не скользит по рельсу и, следовательно, в данный момент равна нулю VР = 0.
В данный момент скорость точки Р равна
, где 
.
Так как в точке Р скорости 
и 
направлены по одной прямой противоположные стороны и VР = 0 , то VPC = VC, откуда получаем, что ω = VC./R, следовательно, VAC = ω R = VC.
Скорость точки А является диагональю квадрата, построенного на взаимно перпендикулярных векторах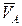 
и 
, модули которых равны, следовательно 
Аналогично определяется скорость точки D. Скорость точки B равна
, при этом скорости и 
равны по модулю и направлены по одной прямой, поэтому VB = 2VC .
Пример2:
Стержень АВ совершает плоское движение, которое можно представить как падение без начальной скорости под действием силы тяжести и вращение вокруг центра тяжести С с постоянной угловой скоростью 
.
Определить уравнения движения точки В, если в начальный момент стержень АВ был горизонтален, а точка В была справа. Ускорение силы тяжести q. Длина стержня 2l. Начальное положение точки С взять за начало координат, а оси координат направить, как указано на рисунке.
Решение. На основании теоремы о разложении движения плоской фигуры на поступательное и вращательное напишем скорость точки В, взяв в качестве полюса точку С: 
.
Спроектируем это геометрическое равенство на оси координат:
(1)
Точка С движется под действием силы тяжести вертикально вниз и проекции ее скорости на оси координат равны 
и 
. (2)
Относительная скорость 
направлена перпендикулярно к стержню АВ, величина же 
. Так как вращение стержня вокруг С равномерное, то угол поворота 
и, следовательно:
(3)
На основании соотношений (2) и(3) уравнения (1) примут вид:
Производя интегрирование и замечая, что в начальный момент t=0, xB=l и yB=0,получим координаты точки В в следующем виде:
(4)
Дата добавления: 2014-12-03; просмотров: 192; Мы поможем в написании вашей работы!; Нарушение авторских прав |