КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Ускорения точек плоской фигуры.
Движение плоской фигуры в своей плоскости можно разложить на поступательное движение вместе с произвольно выбранной точкой, принимаемой за полюс, и вращательное движение вокруг этого полюса.
Следовательно, ускорение любой точки при плоском движении равно геометрической сумме двух ускорений: ускорения выбранного полюса, и ускорения, полученного данной точкой при ее вращательном движении вокруг полюса.
| |
,
где ускорение вращательного движения точки А вокруг точки В раскладывается на нормальное и касательное ускорения:
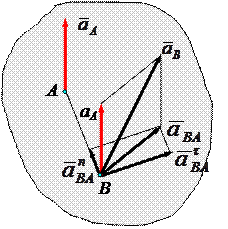
Касательное ускорение вращательного движения точки вокруг полюса направлено перпендикулярно отрезку АВ, соединяющему точку В с полюсом А, и равно
Нормальное ускорение направлено по отрезку ВА к полюсу А и равно
Окончательно, полное ускорение точки В равно геометрической сумме трех ускорений: ускорения выбранного полюса А, нормального и касательного ускорений вращательного движения точки В вокруг этого полюса:
.
Мгновенным центром ускорений называется точка, принадлежащая связанной с плоской фигурой плоскости, ускорение которой в данный момент равно нулю. Если за полюс выбрать мгновенный центр ускорений, то ускорение произвольной точки плоской фигуры определяется как ускорение вращательного движения вокруг мгновенного центра ускорений.
,
где L –мгновенный центр ускорений, 
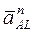- нормальное ускорение, 
- касательное ускорение точки А вращательного движения плоской фигуры вокруг мгновенного центра ускорений.
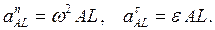
Ускорение 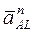- направлено по AL , ускорение - перпендикулярно AL. Ускорение 
точки А образует угол α с отрезком AL соединяющим точку А с мгновенным центром ускорений и равно (рис.12)
,
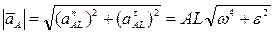Таким образом, если известно ускорение точки А плоской фигуры, то, чтобы найти положение мгновенного центра ускорений, следует это ускорение повернуть вокруг точки А на угол α в сторону вращения фигуры и на полученной прямой отложить расстояние
.
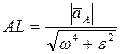Если известны направления ускорений двух точек плоской фигуры, то мгновенный центр ускорений определяется как точка пересечения полученных поворотом этих ускорений на один и тот же угол 
в сторону вращения.
Пример. Центр колеса, катящегося без скольжения по горизонтальной плоскости, в данный момент имеет скорость VC = 2 м/c и ускорение аC = 1,6 м/c. Радиус колеса R = 0,4 м. Определить ускорение точек В и Р (рис. 40).
Так как скорость и ускорение точки С известны, то принимаем точку С за полюс.
Тогда 
,
где 
Мгновенный центр скоростей колеса находится в точке Р – точке касания колеса с неподвижной плоскостью, поэтому
откуда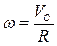 
, при t = 1c, ω = 
Угловое ускорение колеса
при t =1 c,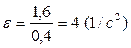 
Тогда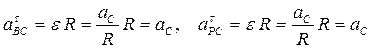 
.
Ускорение точки Р будет направлено к центру колеса точке С и равно
.
Для определения ускорения в точке В спроектируем векторное равенство на горизонтальную ось x и вертикальную ось у: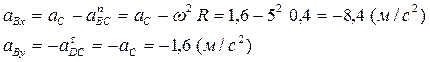 
Лекция №8
Дата добавления: 2014-12-03; просмотров: 500; Мы поможем в написании вашей работы!; Нарушение авторских прав |