
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
СФЕРИЧЕСКОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
Сферическим движением называется движение твердого тела имеющего одну неподвижную точку. Описание такого движения имеет первостепенное значение при анализе работы гироскопов, кораблей, самолётов, снарядов, ракет и небесных тел. Тело, совершающее сферическое движение имеет три степени свободы.
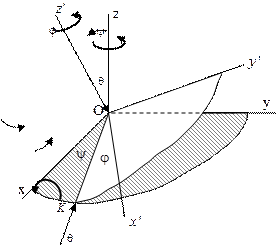
Сферическое движение твердого тела (Углы Эйлера)
Тело, совершающего сферическое движение, привести в заданное положение можно с помощью трех конечных поворотов, называемых углами Эйлера (рис.1.6). Первый поворот произведём вокруг оси 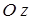 неподвижной системы координат
неподвижной системы координат  угол прецессии
угол прецессии 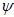 . Второй поворот произведём вокруг линии узлов
. Второй поворот произведём вокруг линии узлов 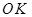 на угол нутации
на угол нутации 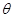 . Третий поворот осуществляется вокруг оси
. Третий поворот осуществляется вокруг оси 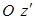 на угол собственного вращения
на угол собственного вращения  . После третьего поворота тело и оси подвижной системы координат
. После третьего поворота тело и оси подвижной системы координат 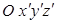 связанные с ним займут заданное положение. При движении тела в каждый момент времени углы Эйлера являются функциями времени:
связанные с ним займут заданное положение. При движении тела в каждый момент времени углы Эйлера являются функциями времени:
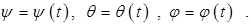
Эти зависимости называются кинематическими уравнениями сферического движения.
Вектор, определяющий положение точки 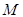 в неподвижной и подвижной системах отсчета, равен
в неподвижной и подвижной системах отсчета, равен
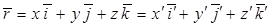 ,
,
а координаты точки связаны при помощи матрицы преобразования

где
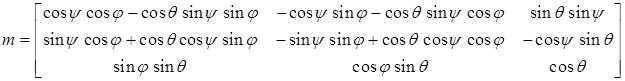
Дата добавления: 2014-12-03; просмотров: 409; Мы поможем в написании вашей работы!; Нарушение авторских прав |