
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Коло змінного синусоїдного струму з ідеальним конденсатором
Під ідеальним конденсатором будемо розуміти такий, у якого активний
опір дорівнює нескінченності. Включимо його в коло з ідеальним генератором (рис.3.16).
 |
Г – генератор;
рА – амперметр;
С – конденсатор.
 Складемо розрахункову схему кола,
Складемо розрахункову схему кола,
прийнявши опори амперметра і з'єднувальних проводів рівними нулю: генератор виробляє синусоїдну е.р.с., змінний струм у колі створює змінне електричне поле в конденсаторі (рис.3.17).
Напруга на ємності
| uс = e. | (3.49) |
Задамося струмом у колі
| i = Im sin (w t + 90°) | (3.50) |
і знайдемо, якою повинна бути в цьому випадку напруга на затисках генератора.
Заряд на обкладках конденсатора
| q = C × uc, | (3.51) |
де q – заряд конденсатора, Кл;
С – ємність конденсатора, Ф;
uc – напруга на конденсаторі, В.
Струм у колі
 , ,
| (3.52) | ||||

| (3.53) (3.54) |
Величину  позначимо xс і назвемо реактивним опором конденсатора,
позначимо xс і назвемо реактивним опором конденсатора,
тобто
 . .
| (3.55) |
Перевіримо одиницю цього опору:
 . .
|
Запишемо закон Ома для максимальних значень, виходячи з виразів (3.54) і (3.55):
 

| (3.56) (3.57) |
Запишемо закон Ома для діючих значень:
 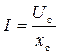

| (3.58) (3.59) |
Представимо графічно напругу і струм у ємності (рис.3.18).
 |
Знайдемо кут зсуву фаз між напругою і струмом у ємності:
| j = |yuС– yi| = |0 –90°| = 90°. |
Таким чином, струм у ємності випереджає напругу за фазою на кут 90°.
Знайдемо миттєву потужність у ємності:

| (3.60) (3.61) |
Величину Qс назвали реактивною потужністю ємності, як одиницю уведено:
| [Qс] = вар. |
Активна потужність у ємності як середнє значення потужності за період:
 . .
| (3.62) |
Отже, енергія в ємності не виділяється, а відбувається обмін енергією між джерелом і приймачем.
Розглянемо цей процес на графіку (рис.3.18). У першу чверть періоду,
коли напруга на обкладках конденсатора зростає, енергія запасається
в електричному полі конденсатора (позитивна заштрихована площа), миттєва потужність позитивна і спрямована від джерела до приймача. В другу чверть періоду, коли напруга зменшується, електричне поле віддає енергію джерелу (негативна
заштрихована площа), миттєва потужність негативна і спрямована від приймача до джерела.
Таким чином, миттєва потужність коливається з подвійною частотою – за половину періоду напруги миттєва потужність здійснює повне коливання.
Приклад 3.8
До ідеального конденсатора підведена напруга uс = 282 sin (wt – 30°) В.
Частота струму в мережі дорівнює 50 Гц. Ємність конденсатора дорівнює 159 мкФ.
Виконати аналіз ділянки кола.
Рішення.
1. Визначаємо ємнісний опір конденсатора за (3.56):
 .
.
2. Визначаємо амплітуду струму за (3.56):
 .
.
3. Визначаємо початкову фазу струму:
yi = yuс + 90 = –30 + 90 = 60°.
4. Записуємо миттєвий струм:
i = 14,1 sin (wt + 60°) А.
5. Визначаємо діюче значення струму за (3.14):
 .
.
6. Визначаємо реактивну потужність за (3.61):
Qс = 20×102 = 2000 вар = 2,0 квар.
Питання для самоконтролю
1. Опишіть фізичні явища, які спостерігаються в ідеальному конденсаторі
в колі синусоїдного струму.
2. Складіть розрахункову схему кола з ідеальним генератором
і ідеальним конденсатором.
3. Запишіть математичний зв'язок між миттєвою напругою,
миттєвим струмом і ємністю в ідеальному конденсаторі.
4. Поясніть фізичну суть ємнісного опору.
Як розрахувати ємнісний опір ідеального конденсатора?
5. Сформулюйте і математично запишіть закон Ома для максимальних
і діючих значень напруги і струму на ділянці кола з ємністю.
6. Запишіть математичний вираз миттєвого струму в ємності,
прийнявши початкову фазу рівною нулю.
7. Запишіть математичний вираз миттєвої напруги на ємності
для зазначеного вище струму.
8. Побудуйте графічно оригінали миттєвої напруги і миттєвого струму
на ділянці кола з ємністю.
9. Зобразите напругу і струм за допомогою векторів.
10. Чому дорівнює кут зсуву фаз у ємності?
11. Отримайте математичний вираз миттєвої потужності в ємності.
З якою частотою коливається миттєва потужність у ємності?
12. Чому дорівнює активна потужність у ємності?
13. Як розрахувати реактивну потужність у ємності? Укажіть її одиницю.
14. Поясните фізичну суть реактивної потужності в ємності.
Завдання для самоконтролю
До ідеального конденсатора підведена напруга
uс = 282 sin (wt + 47°) В. Ємність конденсатора дорівнює 318 мкФ.
Частота струму в колі f = 50 Гц.
1. Знайти реактивний опір конденсатора.
2. Записати миттєве значення струму.
3. Знайти реактивну потужність у ємності.
4. Записати вираз миттєвої потужності в ємності.
5. Зобразити графічно миттєву напругу і миттєву потужність у функції wt.
Дата добавления: 2014-12-03; просмотров: 545; Мы поможем в написании вашей работы!; Нарушение авторских прав |
 .
.