ЗНАХОДЖЕННЯ параметрів моделі методом найменших квадратів

Звернемося до прикладу простої економетричної моделі, де потрібно кількісно оцінити зв’язок між витратами на споживання та доходами сім’ї.Щоб оцінити параметри моделі (16), необхідно сформувати вихідну сукупність спостережень, кожна одиниця якої характеризуватиметься витратами на споживання і доходами сімей. Припустимо, що економетрична модель споживання будується для тієї групи людей, в якій зі збільшенням доходів зростають витрати на споживання, тобто модель має вигляд (16).

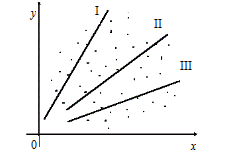Рис. 2.2. Кореляційне поле точок

Зобразимо кожну пару спостережень у системі координат, де величина витрат на споживання відкладається на осі ординат, а доходів — на осі абцис. У результаті дістанемо кореляційне поле точок (рис. 2.2).

На підставі гіпотези про лінійність зв’язку між витратами на споживання і доходом сімей (див. рис.2.2), через кореляційне поле точок можна провести безліч прямих ліній, які різняться між собою параметрами 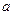і b.

Так, якщо витрати на споживання описуватимуться прямою I, то відхилення їх фактичних значень від розрахункових матимуть переважно знак «мінус». Якщо вони описуватимуться прямою III, то ці відхилення будуть переважно додатними, а якщо прямою II, то кількість від’ємних і додатних відхилень буде приблизно однаковою. Наявність серед відхилень переважно від’ємних чи додатних значень підтверджує, що вони мають невипадковий характер. А це означає: певна пряма лінія не адекватно описує фактичну залежність між витратами на споживання і доходом сімей. Звідси постає задача — застосувати метод найменших квадратів для оцінювання параметрів моделі, щоб відхилення фактичних витрат від розрахункових на основі прямої мали приблизно однакову суму від’ємних і додатних значень, а також були б найменшими. Останнє буде свідчити про те, що розрахункові значення витрат на споживання максимально наближені до фактичних, а це є гарантом вірогідності моделі.

Не доцільно знаходити параметри економетричної моделі, мінімізуючи суму лінійних відхилень фактичних витрат на споживання від розрахункових, бо вона може дорівнювати нулю, якщо сума від’ємних і додатних відхилень буде однаковою. Тому мінімізації підлягає сума квадратів відхилень, і величина її залежатиме безпосередньо від розсіювання точок навколо лінії регресії, а саме:

.

Принцип найменших квадратів відхилень полягає в знаходженні таких 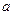і b, для яких 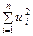найменша. Необхідна умова для цього — перетворення на нуль похідних цієї функції за кожним із параметрів 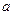і b. Метод, який реалізує принцип найменших квадратів, називається методом найменших квадратів (1МНК). Оскільки

,

то

Виконавши елементарні перетворення, дістанемо систему нормальних рівнянь

(19)

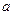Підставимо в систему (19) значення , , , , які можна дістати на підставі сукупності спостережень, і розв’яжемо її відносно невідомих параметрів і b:

Оскільки оцінки найменших квадратів такі, що лінія регресії обов’язково проходить через точку середніх значень ( ), то оцінки параметрів моделі можна знайти дещо інакше.

Поділивши перше рівняння системи (19) на n, дістанемо:

. (20)

Віднімемо (20) від (16):

.

Нехай , і , тоді

,

а відхилення фактичних значень від розрахункових будуть такі:

.

Сума квадратів залишків при цьому

.

Мінімізація цієї суми за невідомим параметром дає співвідношення

. (21)

Крім того, можна помітити, що тобто друга похідна за параметром b від суми квадратів відхилень додатна. Отже, знайдене значення b відповідає мінімуму суми квадратів відхилень.

Параметр a можна обчислити, використавши співвідношення (20):

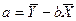. (22)

Співвідношення (21) можна було б дістати також, записавши друге рівняння системи (19) через відхилення кожної змінної від її середнього арифметичного значення, згадавши при цьому, що сума таких відхилень завжди дорівнює нулю.

Приклад 1. Побудувати економетричну модель, яка характеризує залежність витрат на одиницю продукції від рівня фондомісткості продукції. Вихідні дані і відповідні розрахунки для оцінювання параметрів наведені в табл.1.

Таблиця 1

№ п/п	Yі	Xі		XіYі	Xі –	Yі –	(Xі – )2	(Xі – )* (Yі – )	і	uі		(Yі – )2
					-10,8	-4,2	116,64	45,36	48,8	1,2	1,44	17,64
					-25,8	-14,2	665,64	336,36	41,3	-1,3	1,69	201,64
					29,2	10,8	368,64	207,36	63,8	1,2	1,44	116,64
					-0,8	0,8	0,64	-0,64	53,8	1,2	1,44	0,64
					-20,8	-9,2	432,64	181,36	43,8	1,2	1,44	84,64
					-22,8	-12,2	519,64	278,16	42,8	-0,8	0,64	148,84
					9,2	1,8	84,64	16,56	58,8	-2,8	7,84	3,24
					14,2	5,8	201,64	82,36	61,3	-1,3	1,69	33,64
					14,2	9,8	201,64	139,16	61,3	2,7	7,29	96,04
					24,2	10,8	585,64	261,26	66,3	-1,3	1,69	116,64
S								1587,5			26,6	819,6

Нехай залежність між витратами на одиницю продукції і рівнем фондомісткості описується прямою лінією

Y = a + bX + u,

де Y — витрати на одиницю продукції; X — рівень фондомісткості;
u — залишки.

Розрахункові значення витрат на одиницю продукції можна знайти, скориставшись такою моделлю:

.

Щоб оцінити параметри моделі a і b методом 1МНК, запишемо систему нормальних рівнянь

Коефіцієнти для цих рівнянь системи знаходимо за табл.2.1:

Розв’язком системи є параметри a = 3,8; b= 0,5. Економетрична модель має вигляд

Y = 3,8 + 0,5 X + u.

Скориставшись альтернативним способом обчислення параметрів за допомогою відхилень середніх арифметичних, (див. табл.1, стовпці 6–9) на підставі (21) і (22) дістанемо

Зауважимо, що оцінки параметрів моделі згідно з методом 1МНК є досить чутливими до точності розрахунків та адекватності аналітичної форми моделі. Оскільки вільний член моделі a= 3,8 ¹ 0, то рівень витрат на одиницю продукції не є строго пропорційним до рівня фондомісткості. Кількісна оцінка параметра b= 0,5 показує, що граничне збільшення витрат при зростанні фондомісткості продукції на 1 грн. становить 0,5 грн. Еластичність витрат щодо фондомісткості продукції визначається коефіцієнтом еластичності

Значення цього коефіцієнта слід тлумачити так: при збільшенні фондомісткості продукціі на 1 % витрати на одиницю гранично зростуть на 0,93 %.

Питання для самоконтролю.

1.З яких елементів складається математична модель?

2.Назвіть типи математичних моделей. Чим вони різняться між собою?

3.До якого типу математичних моделей належить економетрична модель?

4.Які особливості має економетрична модель?

5.Як треба розуміти сукупність спостережень та її однорідність?

6.Чим забезпечується порівнянність даних у просторі і часі?

7.Як визначається набір змінних для побудови економетричної моделі?

8.Наведіть декілька прикладів економетричних моделей.

9.Дайте тлумачення випадкової складової економетричної моделі.

10.Які методи застосовуються для оцінювання параметрів класичної регресійної моделі?

11.У чому сутність методу найменших квадратів (1МНК)?

12.Запишіть альтернативні варіанти оцінювання параметрів моделі методом 1МНК.

13.Як можна інтерпретувати параметри простої економетричної моделі?