Елементарні дії над матрицями.

Матрицею називається таблиця чисел, яка складається з m рядків і n стовпців:

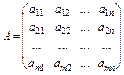
Кількість рядків і стовпців матриці визначає її розміпр m хn.

Якщо , то матриця — прямокутна; якщо m = n — матриця квадратна порядку n (або m ).

Якщо матриця має один стовпець або рядок, то її називають відповідно: матрицею-стовпцем або матрицею-рядком. Загалом такі матриці називають векторами, а саме:

Якщо матриця А має всі нульові елементи, то вона є нульовою:

Квадратна матриця, усі елементи якої, крім елементів головної діагоналі, дорівнюють нулю, називається діагональною:

Якщо в діагональній матриці по головній діагоналі стоять одиниці, а саме

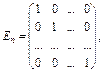
то така матриця називається одиничною n-го порядку.

Якщо в матриці 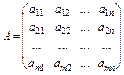поміняти місцями елементи рядків на відповідні елементи стовпців (або навпаки), то дістанемо транспоновану матрицю

Квадратна матриця А називається симетричною, якщо .

Додавання і віднімання виконується тільки для матриць одного й того самого порядку. Якщо і мають однаковий порядок, то матриця суми (різниці) .

Матриця будь-якого порядку А може бути помножена на скаляр l:

При множенні матриці А на скаляр виконуються такі закони:

а)

б)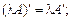

в)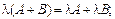

г)

д)

Дві матриці А і В можна помножити одна на одну, якщо кількість стовпців першої матриці дорівнює кількості рядків другої матриці. Кожний елемент матриці-добутку С = АВ є сумою добутків відповідних елементів 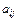і-го рядка на відповідні елементи j-го стовпця:

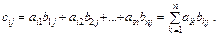
При множенні матриць справджуються такі закони:

а) ;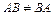

б) (АВ)С = А(ВС);

в) (А + В)С = АС + ВС;

г) С(А + В) = СА + СВ;

д)

е) АE = EA = A;

є)

Добуток матриці на дає скаляр

Якщо вектор 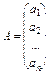, то

і

Квадратна матриця, що задовольняє умову 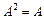, називається ідемпотентною