
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Скалярні характеристики матриць.
Кожна матриця має скалярну характеристику — ранг матриці. Рангом називається максимальна кількість лінійно незалежних векторів-стовпців (рядків) матриці А. Існує й інше означення: найвищий порядок мінора матриці А, який відрізняється від нуля:

m, n – кількість відповідно рядків і стовпців матриці А.
Якщо rgA = min(m,n), то матриця А має повний ранг. Для рангу виконуються такі співвідношення:
а) rgA = rg 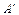 ;
;
б) rg  A = rgA;
A = rgA;
в) rgAB 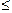 min(rgA, rgB).
min(rgA, rgB).
г) rg 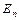 = n .
= n .
Для квадратної матриці існують також скалярні характеристики: слід матриці і її визначник (детермінант).
Слідом матриці розмірності (n х n) є сума елементів, що містяться на її головній діагоналі, тобто
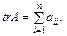
Для сліду виконуються такі співвідношення:
а) 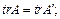
б) 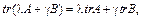 (А і В — матриці однакового порядку);
(А і В — матриці однакового порядку);
в) tr(AB) = tr(BA);
г) 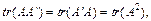 (коли А — симетрична);
(коли А — симетрична);
д) 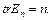
Детермінантом (визначником) квадратної матриці А n-го порядку називається алгебраїчна сума членів, кожний з яких містить n співмножників, узятих по одному і лише по одному з кожного рядка (стовпця) визначника. Позначається:
det A або 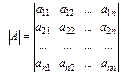 .
.
Визначник (n – 1)-го порядку, в якому викреслені і-й рядок і j-й стовпець, називається мінором елемента 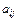 і позначається
і позначається  .
.
Мінор  , який береться зі знаком
, який береться зі знаком  , де і — номер рядка,
, де і — номер рядка,
j — номер стовпця елементa 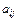 , називається алгебраїчним доповненням цього елемента, а саме:
, називається алгебраїчним доповненням цього елемента, а саме:

Визначник дорівнює сумі попарних добутків елементів будь-якого стовпця (рядка) на їх відповідні алгебраїчні доповнення:
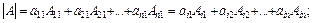
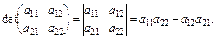
Квадратна матриця, для якої 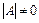 , називається невиродженою. Кожна невироджена матриця має єдину обернену матрицю, для якої виконується:
, називається невиродженою. Кожна невироджена матриця має єдину обернену матрицю, для якої виконується:
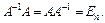
Обернена матриця знаходиться з виразу

де J — приєднaна матриця.
Основні властивості оберненої матриці:
1) 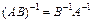 ;
;
2) 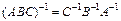 ;
;
3)  ;
;
4)  ;
;
5) 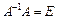 ;
;
6) 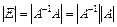 .
.
Матриця, для якої 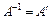 , називається ортогональною.
, називається ортогональною.
Матриці, в яких елементами є окремі підматриці, називаються блоковими:

Розбиваючи матрицю на підматриці, слід додержувати таких правил:
— підматриці, що стоять поруч 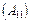 –
– 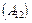 і
і 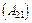 –
–  — повинні мати однакову кількість рядків;
— повинні мати однакову кількість рядків;
— підматриці, які стоять одна під одною 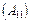 –
– 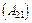 і
і 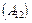 –
–  — повинні мати однакову кількість стовпців.
— повинні мати однакову кількість стовпців.
При додаванні (відніманні) блокових матриць, має насамперед виконуватись умова, що порядок відповідних матриць-доданків однаковий.
При множенні двох блокових матриць кількість стовпців першої матриці має дорівнювати кількості рядків другої матриці. З блоковими матрицями операцію множення виконують за тими самими правилами, що й зі звичайними матрицями.
Кронеккеровий добуток двох матриць 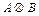

де 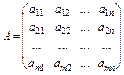 ;
; 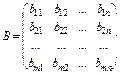 .
.
Якщо матриця 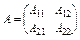 блокова, то
блокова, то 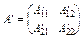 .
.
Обернену блокову матрицю знаходимо за формулою Фробеніуса:
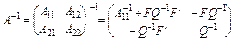 ,
,
де 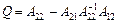 ;
; 
Детермінант блокової матриці А
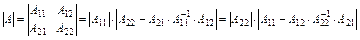
Дата добавления: 2014-12-03; просмотров: 332; Мы поможем в написании вашей работы!; Нарушение авторских прав |