Загальний вид рівняння парної регресії.

Серед багаточисленних зв’язків між економічними показниками завжди можна виділити такий показник, вплив якого на результативну ознаку є основним, найбільш важливим. Щоб виміряти цей зв’язок кількісно, необхідно побудувати економетричну модель з двома змінними (просту модель). Загальний вигляд такої моделі:

Y = f (X, u),

де Y — залежна змінна (результативна ознака); X — незалежна змінна (фактор); u — стохастична складова.

Аналітична форма цієї моделі може бути різною залежно від економічної сутності зв’язків. Найбільш поширені форми залежностей:

;

;

;

,

де а₀, b невідомі параметри моделі.

Неважко переконатись, що наведені нелінійні форми залежностей за допомогою елементарних перетворень приводяться до лінійних. Якщо припустити, що економетрична модель з двома змінними є лінійною:

,

в якій стохастична складова (залишки) має нульове математичне сподівання та постійну дисперсію, то параметри моделі можна оцінити на основі звичайного методу найменших квадратів (1МНК).

В основі методу 1МНК лежить принцип мінімізації суми квадратів залишків моделі:

Реалізація цього принципу дає можливість отримати систему нормальних рівнянь:

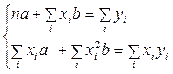
В даній системі n — кількість спостережень, 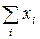, , 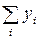, — величини, які можна розрахувати на основі вихідних спостережень над змінними і .

Розв’язавши систему нормальних рівнянь, одержимо оцінки невідомих параметрів моделі і :

.

Достовірність побудованої економетричної моделі можна перевірити, користуючись елементами дисперсійного аналізу. Перш за все слід розрахувати залишки моделі

та знайти їх дисперсію:

,

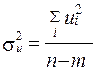де — кількість змінних моделі ( ).

Необхідно визначити стандартну помилку кожного параметра моделі:

(1)

в цій формулі характеризує відповідний діагональний елемент матриці помилок (матриці, оберненої до матриці системи нормальних рівнянь).

На основі коефіцієнта детермінації

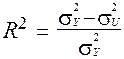
можна зробити висновок про ступінь значущості вимірюваного зв’язку на основі економетричної моделі

.

Оскільки коефіцієнт детермінації R² характеризує, якою мірою варіація залежної змінної визначається варіацією незалежної змінної, то чим ближче R² до одиниці, тим суттєвішим є зв’язок між цими змінними.

Коефіцієнт кореляції R = характеризує тісноту зв’язку між змінними моделі. Він може знаходитись на множині . Чим ближче R до одиниці по модулю, тим тіснішим є зв’язок. Від’ємний знак свідчить про обернений зв’язок, додатній — про прямий.