Аналіз адитивної та мультиплікативної моделі тимчасового ряду.

Ми будемо розглядати моделі лінійного тренду, тобто параметри тренда можливо розрахувати за допомогою моделі лінійної регресії.

Спочатку на основі минулих даних знаходимо сезонну варіацію. Виключив сезонну варіацію за допомогою лінійної регресії знаходимо рівняння тренду. По рівнянню тренда та минулих даних обчислюємо величини похибок. Це середнє абсолютне відхилення MAD= та середньоквадратична похибка МSE= , де e_t - це різниця між фактичними та прогнозними даними в момент часу t, n – кількість даних спостережень.

Для адитивної моделі тимчасового ряду маємо: фактичне значення А= трендові значення Т + сезонна варіація S + похибка Е.

Для мультиплікативної моделі тимчасового ряду маємо: фактичне значення А= трендові значення Т х сезонна варіація S х похибка Е.

Побудова аддитивной і мультиплікативної моделей зводиться до розрахунку значень , і для кожного рівня ряду.

Процес побудови моделі містить у собі наступні кроки.

1) Вирівнювання вихідного ряду методом ковзної середньої.

2) Розрахунок значень сезонної компоненти .

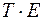3) Усунення сезонної компоненти з вихідних рівнів ряду й одержання вирівняних даних ( ) в адитивній або ( ) у мультиплікативній моделі.

4) Аналітичне вирівнювання рівнів ( ) або ( 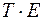) і розрахунок значень з використанням отриманого рівняння тренда.

5) Розрахунок отриманих по моделі значень ( ) або ( ).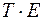

6) Розрахунок абсолютних і відносних помилок. Якщо отримані значення помилок не містять автокореляції, ними можна замінити вихідні рівні ряду і надалі використовувати часовий ряд помилок для аналізу взаємозв'язку вихідного ряду й інших тимчасових рядів.