Оцінка параметрів множинного рівняння регресії.

Для оцінки параметрів рівняння множинної регресії застосовують метод найменших квадратів (1МНК). Для лінійних рівнянь регресії (і нелінійних рівнянь, які зводяться до лінійних) будується система нормальних рівнянь, рішення якої дозволяє одержати оцінки параметрів регресії. У випадку лінійної множинної регресії

y=a+b₁x₁+b₂x₂+…+b_mx_m
система нормальних рівнянь має вигляд:

Для визначення значущості факторів і підвищення точності результату використовується рівняння множинної регресії у стандартизованому масштабі

t_y=

де - стандартизовані змінні

,

для яких середнє значення дорівнює нулю , а середнє квадратичне відхилення дорівнює одиниці.

Коефіцієнти β_i звуться стандартизованими коефіцієнтами регресії.

К рівнянню множинної регресії в стандартизованому масштабі застосовують МНК. Стандартизовані коефіцієнти регресії визначаються з системи рівнянь:

або з системи рівнянь

У парній залежності стандартизований коефіцієнт регресії є не що інше, як лінійний коефіцієнт кореляції r_yx.

Зв'язок коефіцієнтів множинної регресії з стандартизованими коефіцієнтами описується співвідношенням

Параметр а визначається зі співвідношення

a=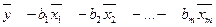

На основі лінійного множинного рівняння регресії

y=a+b₁x₁+b₂x₂+…+b_mx_m+ε

можна знайти частинні рівняння регресії, які зв’язують результативну ознаку з відповідними факторами x_i при закріплених інших, які враховуються в множинній регресії, факторів на середньому рівні. Частинні рівняння регресії мають вигляд:

……………………………………….

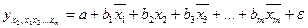
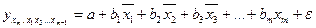
При підстановці в ці рівняння середніх значень відповідних факторів вони приймають вигляду парних рівнянь лінійної регресії, тобто маємо

…………………

де

…………………………

Приклад 1. Оцінити параметри економетричної моделі, що характеризує залежність між тижневими витратами на харчування, загальними витратами та розміром сім’ї. Вихідні дані наведені в табл.1.

Розв’язання. Запишемо економетричну модель:

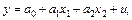
де y, 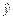— відповідно фактичні та розрахункові значення тижневих витрат на харчування за моделлю; x₁ — загальні витрати; x₂ — розмір сім’ї; u — залишки; , , — оцінка параметрів моделі.

Оператор оцінювання параметрів моделі за 1МНК має вигляд

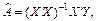
де ;

— матриця, транспонована до матриці X.

Матриця X крім двох векторів незалежних змінних містить вектор одиниць. Він дописується в цій матриці ліворуч тоді, коли економетрична модель має вільний член. не дописуючи такого вектора одиниць, вільний член можна обчислити, скориставшись рівністю:

де — середнє значення залежної змінної; , — середні значення незалежних змінних і .

Згідно з оператором оцінювання знайдемо:

1)

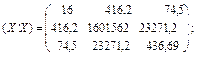
2)

3) ;

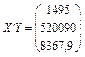4)

Отже, економетрична модель має вигляд

Знайдені методом 1МНК оцінки параметрів такі: 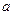= 8,8;b₁=0,2; b₂= 6,97, тобто

.