Значущість оцінок параметрів моделі

Перевіримо значущість оцінок параметрів В і знайдемо для них довірчі інтервали, припустивши для цього, що залишки u нормально розподілені, тобто . Тоді параметри моделі В задовольняють багатовимірний нормальний розподіл:

(17)

Коли відома величина , то цей результат можна бути використати для перевірки значущості елементів вектора та оцінювання довірчих інтервалів елементів цього вектора. Проте дисперсія невідома, а отже, потрібно розглянути методи її знаходження.

Для цього визначимо залишки:

(18)

Таким чином, залишки, які можна дістати на підставі експериментальних даних, записано у вигляді лінійних функцій від невідомих залишків . Тоді суму квадратів відхилень подамо у вигляді

(19)

де N— симетрична ідемпотентна матриця.

У цих перетвореннях ми виходили з того, що N є симетричною ідемпотентною матрицею, оскільки E_n — одинична матриця, а — симетрична розміром n ´ m.

Знайдемо математичне сподівання для обох частин рівняння (19) і застосуємо спочатку властивість, яка полягає в тому, що , де — слід матриці N, а далі — властивість комутативності добутку матриць відносно операцій обчислення сліду матриці.

З огляду на сказане маємо:

(20)

У цьому співвідношенні матриця має порядок , добуток 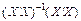дорівнює 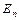, а її слід дорівнює . Звідси

. (21)

Співвідношення (21) дає нам незміщену оцінку дисперсії залишків.

Нарешті, лишилося показати, що сума квадратів залишків розподілена незалежно від В. Для цього знайдемо коваріацію залишків:

(22)

Оскільки 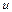і В є лінійні функції від нормально розподілених змінних, то вони також розподілені нормально і, як було показано, їх коваріації дорівнюють нулю.

Це дає нам змогу скористатися t-розподілом для перевірки гіпотез відносно істотності кожного з параметрів економетричної моделі

Перевірку гіпотези виконаємо згідно з t-критерієм:

, (23)

де — діагональний елемент матриці 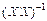. Знаменник відношення (23) — називається стандартною помилкою оцінки параметра моделі.

Обчислене значення t-критерію порівнюється з табличним при вибраному рівні значущості і ступенях свободи. Якщо t факт > t табл, то відповідно оцінка параметра економетричної моделі є достовірною.

На основі t-критерію і стандартної помилки побудуємо довірчі інтервали для параметрів :

(24)

Питання для самоконтролю.

1. Коли для оцінки параметрів моделі можна застосувати 1МНК?

2. Запишіть оператор оцінювання 1МНК. Як його можна дістати?

3. Які властивості повинні мати оцінки параметрів економетричної моделі?

4. Чим відрізняються коефіцієнти парної та часткової кореляції?

5. запишіть співвідношення між коефіцієнтами кореляції і детермінації.

6. Як визначаються дисперсія залишків, загальна дисперсія і дисперсія регресії? Який між ними зв’язок?

7. Як визначається F-критерій? Для чого він застосовується?

8. Покажіть залежність між F-критерієм і .

9. Як оцінити вірогідність коефіцієнта кореляції?

10. Доведіть, чому для визначення значущості параметрів моделі можна застосувати t-критерій?

11. Як обчислюється t-критерій?