
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Алгоритм Феррара - Глобера
Найповніше дослідити мультиколінеарність можна за допомогою алгоритму Феррара — Глобера. Цей алгоритм має три види статистичних критеріїв, згідно з якими перевіряється мультиколінеарність всього масиву незалежних змінних (  - «хі» — квадрат); кожної незалежної змінної з рештою змінних (F-критерій); кожної пари незалежних змінних (t-критерій).
- «хі» — квадрат); кожної незалежної змінної з рештою змінних (F-критерій); кожної пари незалежних змінних (t-критерій).
Усі ці критерії при порівнянні з їх критичними значеннями дають змогу робити конкретні висновки щодо наявності чи відсутності мультиколінеарності незалежних змінних.
Опишемо алгоритм Феррара — Глобера.
Крок 1. Стандартизація (нормалізація) змінних.
Позначимо вектори незалежних змінних економетричної моделі через  . Елементи стандартизованих векторів обчислимо за формулою:
. Елементи стандартизованих векторів обчислимо за формулою:
 (2)
(2)
де 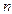 — число спостережень
— число спостережень  ;
;
 — число пояснювальних змінних,
— число пояснювальних змінних, 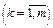 ;
;
 — середнє арифметичне k-ї пояснювальної змінної;
— середнє арифметичне k-ї пояснювальної змінної;
 — дисперсія k-ї пояснювальної змінної.
— дисперсія k-ї пояснювальної змінної.
Крок 2. Знаходження кореляційної матриці
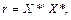 (3)
(3)
де 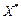 — матриця стандартизованих незалежних (пояснювальних) змінних,
— матриця стандартизованих незалежних (пояснювальних) змінних,  — матриця, транспонована до матриці
— матриця, транспонована до матриці 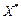 .
.
Крок 3. Визначення критерію  («хі»-квадрат):
(«хі»-квадрат):
 (4)
(4)
де 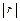 — визначник кореляційної матриці r.
— визначник кореляційної матриці r.
Значення цього критерію порівнюється з табличним при 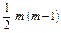 ступенях свободи і рівні значущості
ступенях свободи і рівні значущості 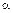 . Якщо
. Якщо  то в масиві пояснювальних змінних існує мультиколінеарність.
то в масиві пояснювальних змінних існує мультиколінеарність.
Крок 4. Визначення оберненої матриці:
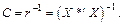 (5)
(5)
Крок 5. Очислення F-критеріїв:
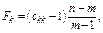 (6)
(6)
де 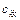 — діагональні елементи матриці C. Фактичні значення критеріїв порівнюються з табличними при n – m і m – 1 ступенях свободи і рівні значущості a. Якщо Fkфакт > Fтабл, то відповідна k-та незалежна змінна мультиколінеарна з іншими.
— діагональні елементи матриці C. Фактичні значення критеріїв порівнюються з табличними при n – m і m – 1 ступенях свободи і рівні значущості a. Якщо Fkфакт > Fтабл, то відповідна k-та незалежна змінна мультиколінеарна з іншими.
Коефіцієнт детермінації для кожної змінної
 (7)
(7)
Крок 6. Знаходження частинних коефіцієнтів кореляції:
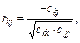 (8)
(8)
де 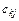 — елемент матриці C, що міститься в k-му рядку і j-му стовпці;
— елемент матриці C, що міститься в k-му рядку і j-му стовпці; 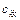 i
i  — діагональні елементи матриці C.
— діагональні елементи матриці C.
Крок 7. Обчислення t-критеріїв:
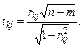 (9)
(9)
Фактичні значення критеріїв 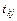 порівнюються з табличними при
порівнюються з табличними при 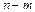 ступенях свободи і рівні значущості
ступенях свободи і рівні значущості  . Якщо tkj(ф) > t табл, то між незалежними змінними
. Якщо tkj(ф) > t табл, то між незалежними змінними  і
і 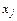 існує мультиколінеарність.
існує мультиколінеарність.
Розглянемо застосування алгоритму Феррара — Глобера для розв’язування конкретної задачі.
Приклад 1. На середньомісячну заробітну плату впливає ряд чинників. Вирізнимо серед них продуктивність праці, фондомісткість та коефіцієнт плинності робочої сили. Щоб побудувати економетричну модель заробітної плати від згаданих чинників згідно з методом найменших квадратів, потрібно переконатися, що продуктивність праці, фондомісткість та коефіцієнт плинності робочої сили як незалежні змінні моделі — не мультиколеніарні.
Вихідні дані наведені у табл.1.
Таблиця 1
| Номер цеху | Продуктивність праці, людино-днів | Фондомісткість, млн грн. | Коефіцієнт плинності робочої сили, % |
| 0,89 | 19,5 | ||
| 0,43 | 15,6 | ||
| 0,70 | 13,5 | ||
| 0,61 | 9,5 | ||
| 0,51 | 23,5 | ||
| 0,51 | 12,5 | ||
| 0,65 | 17,5 | ||
| 0,43 | 14,5 | ||
| 0,51 | 14,5 | ||
| 0,92 | 7,5 |
Дослідити наведені чинники на наявність мультиколеніарністі.
Дата добавления: 2014-12-03; просмотров: 287; Мы поможем в написании вашей работы!; Нарушение авторских прав |