
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Розв’язання.
Крок 1. Нормалізація змінних.
Позначимо вектори незалежних змінних — продуктивності праці, фондомісткості, коефіцієнтів плинності робочої сили — через  . Елементи стандартизованих векторів обчислимо за формулою:
. Елементи стандартизованих векторів обчислимо за формулою:

де n — кількість спостережень, n = 10; m — число незалежних змінних, m = 3;  — середнє арифметичне значення вектора
— середнє арифметичне значення вектора  ;
;  — дисперсія змінної
— дисперсія змінної  .
.
Із формули бачимо, що спочатку потрібно обчислити середні арифметичні для кожної пояснювальної змінної:


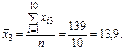
Усі розрахункові дані для стандартизації змінних 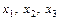 згідно з поданими співвідношеннями наведено в табл.2.
згідно з поданими співвідношеннями наведено в табл.2.
Таблиця 2

| 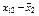
| 
| 
| 
| 
| 
| 
| 
|
| 3,3 | 0,004 | -3,4 | 10,89 | 0,000016 | 11,56 | 0,2487 | 0,0091 | -0,2518 |
| 0,3 | -0,156 | 1,6 | 0,09 | 0,024336 | 2,56 | 0,0226 | -0,3531 | 0,1185 |
| 1,6 | 0,114 | -0,4 | 1,89 | 0,012995 | 0,16 | 0,0980 | 0,2580 | -0,0296 |
| 2,3 | 0,024 | -4,4 | 5,29 | 0,000576 | 19,36 | 0,1733 | 0,0543 | -0,3258 |
| -3,7 | -0,676 | 9,6 | 13,89 | 0,005776 | 92,16 | -0,2788 | -0,1720 | 0,7108 |
| 5,3 | -0,078 | -1,4 | 28,09 | 0,005776 | 1,96 | 0,3994 | -0,1720 | -0,1037 |
| 0,3 | 0,064 | -3,6 | 0,09 | 0,004096 | 12,96 | 0,0226 | 0,1448 | 0,2666 |
| -4,7 | -0,156 | 0,6 | 22,09 | 0,024336 | 0,35 | -0,3541 | -0,3531 | 0,0444 |
| -8,7 | -0,076 | 0,6 | 75,89 | 0,005778 | 0,35 | -0,6556 | -0,1720 | 0,0444 |
| 4,3 | 0,334 | -6,4 | 14,49 | 0,111555 | 40,95 | 0,3240 | 0,7559 | -0,4739 |
| Всього | 176,1 | 0,19524 | 182,4 |
Дисперсії кожної незалежної змінної мають такі значення:



Тоді знаменник для стандартизації кожної незалежної змінної буде такий:
 :
: 
 :
: 
 :
: 
Матриця стандартизованих змінних подається у вигляді:
 .
.
Крок 2. Знаходження кореляційної матриці:

де  — матриця, транспонована до
— матриця, транспонована до  .
.
Ця матриця симетрична і має розмір 3 х 3.
Для даної задачі

Кожний елемент цієї матриці характеризує тісноту зв’язку однієї незалежної змінної з іншою. Оскільки діагональні елементи характеризують тісноту зв’язку кожної незалежної з цією самою змінною, то вони дорівнюють одиниці. Зауважимо, що при знаходженні добутку матриць 
 за рахунок зміщеності коефіцієнтів парної кореляції числові значення діагональних елементів можуть наближатись до одиниці. Якщо це так, то вони заміняються одиницями, а інші значення матриці r збільшуються на величину, що визначається як різниця між одиницею і діагональним елементом.
за рахунок зміщеності коефіцієнтів парної кореляції числові значення діагональних елементів можуть наближатись до одиниці. Якщо це так, то вони заміняються одиницями, а інші значення матриці r збільшуються на величину, що визначається як різниця між одиницею і діагональним елементом.
Інші елементи матриці r дорівнюють:



тобто вони є парними коефіцієнтами кореляції між пояснювальними змінними. Користуючись цими коефіцієнтами, можна зробити висновок, що між змінними  існує зв’язок. Але чи можна стверджувати, що цей зв’язок є виявленням мультиколінеарності, а через це негативно впливатиме на оцінку економетричної моделі?
існує зв’язок. Але чи можна стверджувати, що цей зв’язок є виявленням мультиколінеарності, а через це негативно впливатиме на оцінку економетричної моделі?
Щоб відповісти на це запитання, потрібно ще раз звернутися до алгоритму Феррара — Глобера і знайти статистичні критерії оцінки мультиколінеарності.
Крок 3. Обчислимо детермінант кореляційної матриці r і критерій  :
:
а) 
б) 
При ступені свободи  і рівні значущості
і рівні значущості  = 0,01 критерій
= 0,01 критерій  табл = 11,34. оскільки
табл = 11,34. оскільки  факт <
факт < 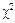 табл, доходимо висновку, що в масиві змінних не існує мультиколінеарності.
табл, доходимо висновку, що в масиві змінних не існує мультиколінеарності.
Крок 4. Знайдемо матрицю, обернену до матриці r:


Крок 5. Використовуючи діагональні елементи матриці C, обчислимо F-критерії:



Для рівня значущості  = 0,05 і ступенів свободи
= 0,05 і ступенів свободи  = 7 і
= 7 і  = 2 критичне (табличне) значення критерію F = 4,74.
= 2 критичне (табличне) значення критерію F = 4,74.
Оскільки
F1факт < Fтабл;
F2факт < Fтабл;
F3факт < Fтабл,
то ні одна з незалежних змінних не мультиколінеарна з двома іншими.
Щоб визначити наявність попарної мультиколінеарності, продовжимо дослідження і перейдемо до кроку 6.
Крок 6. Обчислимо частинні коефіцієнти кореляції, скориставшись елементами матриці C:


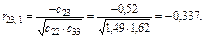
Частинні коефіцієнти кореляції характеризують тісноту зв’язку між двома змінними за умови, що третя не впливає на цей зв’язок.
Порівнявши частинні коефіцієнти кореляції з парними, які було наведено раніше, можна помітити, що частинні коефіцієнти значно менші за парні. Це ще раз показує, що на підставі парних коефіцієнтів кореляції не можна зробити висновків про наявність мультиколінеарності чи її відсутність.
Крок 7. Визначимо t-критерій на основі частинних коефіцієнтів кореляції.
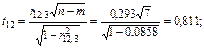


Табличне значення t-критерію при  = 7 ступенях свободи і рівні значущості a = 0,05 дорівнює 1,69. Усі числові значення t-критеріїв, знайдених для кожної пари змінних, менші за їх табличні значення. Звідси робимо висновок, що всі пари незалежних змінних не є мультиколінеарними.
= 7 ступенях свободи і рівні значущості a = 0,05 дорівнює 1,69. Усі числові значення t-критеріїв, знайдених для кожної пари змінних, менші за їх табличні значення. Звідси робимо висновок, що всі пари незалежних змінних не є мультиколінеарними.
Отже, незважаючи на те, що між пояснювальними змінними досліджуваної моделі існує лінійна залежність, це не мультиколінеарність, тобто негативного впливу на кількісні оцінки параметрів економетричної моделі, не буде.
Якщо F-критерій більший за табличне значення, тобто коли k-та змінна залежить від усіх інших у масиві, то необхідно вирішувати питання про її вилучення з переліку змінних.
Якщо  — критерій більший за табличний, то ці дві змінні (
— критерій більший за табличний, то ці дві змінні (  і
і  ) тісно пов’язані одна з одною. Звідси, аналізуючи рівень обох видів критеріїв
) тісно пов’язані одна з одною. Звідси, аналізуючи рівень обох видів критеріїв  і
і  , можна зробити обгрунтований висновок про те, яку зі змінних необхідно вилучити з дослідження або замінити іншою. Проте заміна масиву незалежних змінних завжди має узгоджуватись з економічною доцільністю, що випливає з мети дослідження.
, можна зробити обгрунтований висновок про те, яку зі змінних необхідно вилучити з дослідження або замінити іншою. Проте заміна масиву незалежних змінних завжди має узгоджуватись з економічною доцільністю, що випливає з мети дослідження.
Найпростіше позбутися мультиколінеарності в економетричній моделі можна, відкинувши одну зі змінних мультиколінеарної пари. Але на практиці вилучення якогось чинника часто суперечить логіці економічних зв’язків. Тоді можна перетворити певним чином пояснювальні змінні моделі:
а) взяти відхилення від середньої;
б) замість абсолютних значень взяти відносні;
в) стандартизувати пояснювальні змінні
і т. iн.
За наявності мультиколінеарності змінних потрібно звертати увагу й на специфікацію моделі. Іноді заміна однієї функції іншою, якщо це не суперечить апріорній інформації, дає змогу уникнути явища мультиколінеарності.
Коли жодний з розглянутих способів не дає змоги позбутися мультиколінеарності, то параметри моделі слід оцінювати за методом головних компонентів.
3.2. Метод головних компонентів
Цей метод призначений для оцінювання моделей великого розміру, а також для оцінки параметрів моделі, якщо до неї входять мультиколінеарні змінні.
Існують різні модифікації методу головних компонентів, які різняться між собою залежно від того, що береться за основу при визначенні ортогональних змінних — коваріаційна чи кореляційна матриця незалежних змінних.
Нехай маємо матрицю Х, яка описує незалежні змінні моделі. Оскільки спостереження, що утворюють матрицю Х, як правило, корельовані між собою, то можна поставити питання про кількість реально незалежних змінних, які входять до цієї матриці.
Точніше, ідея методу полягає в тому, щоб перетворити множину змінних Х на нову множину попарно некорельованих змінних, серед яких перша відповідає максимально можливій дисперсії, а друга — максимально можливій дисперсії в підпросторі, який є ортогональним до першого, і т.д.
Нехай нова змінна запишеться:

У матричній формі
 (10)
(10)
де  — вектор значень нової змінної;
— вектор значень нової змінної; 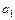 — m-вимірний власний вектор матриці
— m-вимірний власний вектор матриці  .
.
Суму квадратів елементів вектора подамо у вигляді:
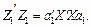 (11)
(11)
Звідси необхідно вибрати такий вектор 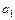 , який максимізуватиме
, який максимізуватиме  , але на вектор
, але на вектор 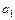 треба накласти обмеження, щоб він не став дуже великим. Тому ми його нормуємо, наклавши обмеження:
треба накласти обмеження, щоб він не став дуже великим. Тому ми його нормуємо, наклавши обмеження:
 (12)
(12)
Оскільки Z1 = Xa1, то максимізація a1 буде максимізувати Z1, а Z1 характеризує вклад змінної Z1 в загальну дисперсію.
Задача тепер полягає в тому, щоб максимізувати  за умов (12). Побудуємо функцію Лагранжа:
за умов (12). Побудуємо функцію Лагранжа:

де  — множник Лагранжа.
— множник Лагранжа.
Узявши  , дістанемо
, дістанемо
 . (13)
. (13)
Звідси бачимо, що 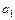 — власний вектор матриці
— власний вектор матриці  , який відповідає характеристичному числу
, який відповідає характеристичному числу  .
.
Підставивши значення (13) у (11), дістанемо:
 (14)
(14)
Отже, потрібно для значення  вибрати найбільший характеристичний корінь матриці
вибрати найбільший характеристичний корінь матриці  . За відсутності мультиколінеарності матриця
. За відсутності мультиколінеарності матриця  буде додатно визначеною і, відповідно, її характеристичні корені будуть додатними. Першим головним компонентом матриці X буде вектор Z1.
буде додатно визначеною і, відповідно, її характеристичні корені будуть додатними. Першим головним компонентом матриці X буде вектор Z1.
Визначимо тепер  . При цьому вектор
. При цьому вектор 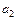 має максимізувати вираз
має максимізувати вираз  за таких умов:
за таких умов:
1)  ;
;
2) 
Друга умова забезпечить відсутність кореляції між  і
і  , бо коваріація між
, бо коваріація між  і
і  подається у вигляді
подається у вигляді  , причому вона дорівнює нулю лише тоді, коли
, причому вона дорівнює нулю лише тоді, коли  .
.
Для розв’язування цієї задачі функцію Лагранжa запишемо у вигляді

де 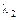 і
і  — множники Лагранжa.
— множники Лагранжa.
Узявши  і
і  , дістанемо
, дістанемо  де для значення
де для значення 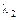 треба вибрати другий за величиною характеристичний корінь матриці
треба вибрати другий за величиною характеристичний корінь матриці  .
.
Цей процес триває доти, доки всі m характеристичних значень матриці  не будуть знайдені; знайдені m власних векторів матриці
не будуть знайдені; знайдені m власних векторів матриці  об’єднаємо в ортогональну матрицю:
об’єднаємо в ортогональну матрицю:
 .
.
Отже, головні компoненти матриці X задаються матрицею
 (15)
(15)
розміром n ´ m.
 . (16)
. (16)
Вираз (16) означає, що головні компоненти дійсно попарно некорельовані, а їх дисперсії визначаються так:
 (17)
(17)

Співвідношення 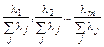 характеризують пропорційний внесок кожного з векторів у загальну варіацію змінних X, причому оскільки ці компоненти ортогональні, сума всіх внесків дорівнює одиниці.
характеризують пропорційний внесок кожного з векторів у загальну варіацію змінних X, причому оскільки ці компоненти ортогональні, сума всіх внесків дорівнює одиниці.
Зауважимо, що вектори вихідних даних (матриця X) повинні мати однакові одиниці вимірювання, бо в противному разі дуже важко дати змістовне тлумачення поняттю загальної варіації змінних X і розкладанню цієї варіації на складові, виконаному відповідно до внеску кожного з векторів, якими подаються головні компоненти.
Іноді буває важко надати конкретного змісту знайденим головним компонентам. Для цього можна обчислити коефіцієнти кореляції кожного компонента з різними змінними X. Так, наприклад, візьмемо перший головний компонент Z1 і знайдемо коефіцієнти його кореляції її з усіма змінними X. Для цього потрібно обчислити перехресні добутки між головним компонентом Z1 і кожною з пояснювальних змінних X. Оскільки

маємо коефіцієнти кореляції для першого компонента:
 (18)
(18)
У загальному випадку коефіцієнт кореляції між 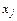 і
і 
 (19)
(19)
Частка різних головних компонентів в варіації 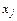 визначається показником
визначається показником  , а оскільки компоненти не корелюють один з одним, то сума їх часток дорівнює одиниці.
, а оскільки компоненти не корелюють один з одним, то сума їх часток дорівнює одиниці.
Визначивши всі головні компоненти і відкинувши ті з них, які відповідають невеликим значенням характеристичних коренів, знаходимо зв’язок залежної змінної Y з основними головними компонентами, а далі з допомогою оберненого перетворення повертаємося від параметрів моделі з головними компонентами до знаходження оцінок параметрів змінних X.
Приклад 2. Нехай для п’яти змінних матриці X знайдено п’ять головних компонентів. Порівнявши їх значення, вибираємо лише два:
 (20)
(20)
Тоді модель, що характеризує зв’язок між Y, Z1 i Z2, має вигляд:
 (21)
(21)
Підставимо в (21) значення головних компонентів із (20):
 (22)
(22)
У разі, коли було б збережено всі головні компоненти, коефіцієнти рівняння (22) були б такі самі, як коефіцієнти, знайдені на основі прямої регресії Y на всі змінні X.
Розглянемо, як обчислити параметри моделі з головними компонентами:

Звідси  (23)
(23)
Оскільки  , то, підставивши цей вираз у (23), дістанемо:
, то, підставивши цей вираз у (23), дістанемо:

тобто



. . . . . . . . . .

 , тому
, тому  нормально і незалежно розподілені навколо b.
нормально і незалежно розподілені навколо b.
Алгoритм головних компонентів
Крок 1. Нормалізація всіх пояснювальних змінних:

Крок 2. Обчислення кореляційної матриці

Крок 3. Знаходження характеристичних чисел матриці r з рівняння

де E — одинична матриця розміром m ´ m.
Крок 4. Власні значення  упорядковуються за абсолютним рівнем вкладу кожного головного компонента до загальної дисперсії.
упорядковуються за абсолютним рівнем вкладу кожного головного компонента до загальної дисперсії.
Крок 5. Обчислення власних векторів  розв’язуванням системи рівнянь
розв’язуванням системи рівнянь

за таких умов:
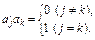
Крок 6. Знаходження головних компонентів — векторів
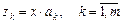
Головні компоненти мають задовольняти умови:
 ;
;
 ;
;

Крок 7. Визначення параметрів моделі  :
:

Крок 8. Знаходження параметрів моделі  :
:

Питання для самоконтролю.
1. Що означає мультиколінеарність змінних?
2. ознаки мультиколінеарності.
3. Як впливає наявність мультиколінеарність змінних на оцінку параметрів моделі?
4. Які статистичні критерії використовуються для виявлення мультиколінеарністі?
5. Дайте коротку характеристику алгоритму Феррара — Глобера.
6. На чому грунтується метод головних компонентів? Коли він застосовується?
7. Як обчислити головні компоненти і які умови вони задовольняють?
8. Як оцінюються параметри моделі на основі головних компонентів?
Дата добавления: 2014-12-03; просмотров: 429; Мы поможем в написании вашей работы!; Нарушение авторских прав |