Множинний коефіцієнт кореляції і детермінації

Тіснота зв’язку загального впливу всіх незалежних змінних на залежну визначається коефіцієнтами детермінації і множинної кореляції.

Щоб дати метод їх розрахунку необхідно показати, що варіація залежної змінної (Y) навколо свого вибіркового середнього значення ( 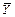)* може бути розкладена на дві складові:

1) варіацію розрахункових значень ( 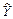) навколо середнього значення ;

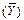2) варіацію розрахункових значень ( 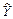) навколо фактичних (Y).

Необхідні при цьому обчислення зведемо в табл.2.

Таблиця 2

Джерело варіації	Сума квадратів відхилень	Ступені свободи	Середнє квадратів відхилень або дисперсія
Факторна ( )
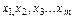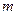
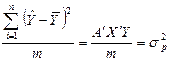
Залишок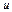
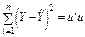
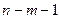
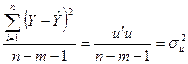
Загальна варіація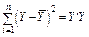

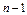
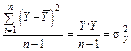
Зауважимо, що всі змінні Y i X взяті як відхилення від свого середнього значення.

Використаємо середні квадратів відхилень (дисперсії) (див. табл. 2) і запишемо формулу для обчислення коефіцієнта детермінації:

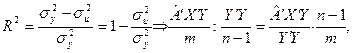(8)

або, не враховуючи ступенів свободи:

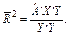(9)

Оскільки у (8) задані незміщені оцінки дисперсії з урахуванням числа ступенів свободи, то коефіцієнт детермінації може зменшуватись при введені в модель нових незалежних змінних. Тоді як для коефіцієнта детермінації, обчисленого без урахування поправки (n – 1/m – 1) на число ступенів свободи (9), коефіцієнт детермінації ніколи не зменшується. Залежність між цими двома коефіцієнтами можна подати так:

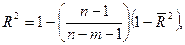(10)

де — коефіцієнт детермінації з урахуванням числа ступенів свободи;

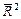— коефіцієнт детермінації без урахування числа ступенів свободи.

Для функції з двома і більше незалежними змінними коефіцієнт детермінації може набувати значень на множині 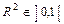. Числове значення коефіцієнта детермінації характеризує, якою мірою варіація залежної змінної ( ) визначається варіацією незалежних змінних. Чим ближчий він до одиниці, тим більше варіація залежної змінної визначається варіацією незалежних змінних.

Множинний коефіцієнт кореляції:

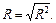
Він характеризує тісноту зв’язку усіх незалежних змінних із залежною.

Для множинного коефіцієнта кореляції з урахуваннням і без урахуванння числа ступенів свободи характерна така сама зміна числового значення, як і для коефіцієнта детермінації.

Розглянемо альтернативний спосіб обчислення коефіцієнтів детермінації і кореляції, коли система нормальних рівнянь будується на основі коефіцієнтів парної кореляції .

У такому разі оцінку параметрів моделі можна записати:

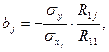(11)

де 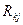— алгебраїчне доповнення матриці до елемента .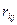

Сума квадратів відхилень (залишків) також може бути виражена через алгебраїчне доповнення матриці :

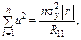
де 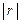— визначник кореляційної матриці. А це, у свою чергу, дає нам альтернативний вираз для коефіцієнта детермінації:

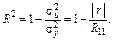(12)

Ще один альтернативний метод розрахунку коефіцієнтів детермінації на основі матриці можна подати у вигляді

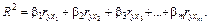(13)

Звідси коефіцієнт кореляції

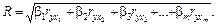(14)