Системи лінійних рівнянь.

Система лінійних рівнянь в матричному вигляді записується АХ = В, дe

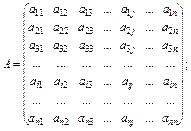
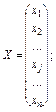
Якщо А — невироджена матриця, то розв’язок системи АХ = В знаходиться як

.

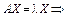
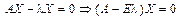Система лінійних рівнянь АХ = 0, називається однорідною. Вона має нетривіальні розв’язки, якщо . Система рівнянь має нетривіальний розв’язок, якщо Останнє рівняння називають характеристичним рівнянням матриці А.

Корені рівняння 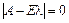є характеристичними коренями (характеристичними числами, власними значеннями) матриці А.

Вектори X_k, які є розв’язком системи для відповідного характеристичного кореня 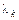, називаються власними векторами матриці А. Добуток

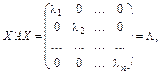
де Х — матриця власних векторів А;

— характеристичні корені матриці А.

Приклад 1. Знайти розвязок системи рівнянь.

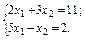
У матричному виді:

AX = B;

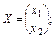
отже,

.

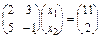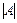= –2 – 15 = –17 — матриця невироджена.

Запам’ятайте: для матриці обернена матриця має вигляд .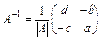

.

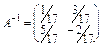Отже,

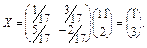
Розв’язок системи: = 1; = 3.

Розглянемо однорідну систему лінійних рівнянь:

АХ = 0

Нехай А — квадратна матриця n-го порядку; Х — вектор-стовпець розміру n х1.

Тривіальний розв’язок має вигляд: 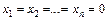. Нетривіальний розв’язок може існувати лише за умови, що визначник матриці А дорівнює нулю:

Коли це так, то система матиме безліч розв’язків. Їх можна нормувати, вимагаючи, наприклад, щоб виконувалася рівність

Приклад 2. Знайти нетривіальні розв’язки однорідної системи рівнянь.

(1)

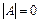, це означає, що задана система має нетривіальні розв’язки.

Матрицю А можна записати як систему трьох векторів:

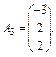
Систему (1) подамо як лінійну комбінацію вектора :

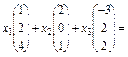
(2)

Неважко побачити, що 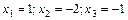; розв’язками системи (1) будуть і ці самі значення, помножені на будь-які числа, які задовольняють рівняння (2). Отже, система векторів є лінійно залежною, причому розв’язки системи лінійних рівнянь (1) є коефіцієнтами лінійної комбінації вектора :

Приклад 3. Знайти характеристичні корені матриці А.

Запишемо рівняння або

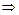
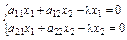
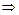
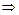
(3)

Запишемо характеристичне рівняння для системи (3):

(4)

Отже,

. (5)

Нехай матриця А — симетрична, тоді і характеристичні корені цієї матриці

. (6)

Підставивши поступово в систему (3), знайдемо власні вектори X₁, X₂ матриці А.

Приклад 4. Знайти характеристичні корені і власні вектори X₁, X₂ матриці А:

.

Матриця А симетрична. Для визначення застосуємо (5):

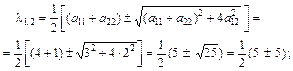
Щоб знайти власні вектори 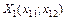i , розв’яжемо для кожного систему рівнянь (3).

Нехай, тоді

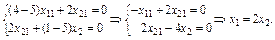(7)

Нормалізуємо вектор , зводячи його довжину до 1, тобто:

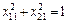(8)

Підставимо (7) в (8):

Звідси,

Власний вектор

(9)

Для знаходження власного вектора покладемо .

Система (3) запишеться у вигляді

(10)

Нормалізуємо вектор , звівши його довжину до 1, тобто:

(11)

Підставивши (10) у (11), дістанемо:

Власний вектор

(12)

Зауважимо, що оскільки , то власні вектори X₁ і X₂ ортогональні, тобто лінійно незалежні:

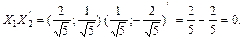
Перевіримо, чи виконується (3):

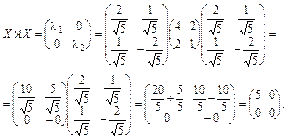
Отже, співвідношення справді переводить матрицю А в діагональ­ну матрицю . Це підтверджує правильність наведених обчислень.