МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ. ЗДР з невідомою функцією у(х), в яку входять похідні цієї функції навіть до , називаються ЗДР n-го порядку

ЗДР з невідомою функцією у(х), в яку входять похідні цієї функції навіть до , називаються ЗДР n-го порядку. Якщо маємо таке рівняння, то для коректної постановки задачі Коші потрібно задати n початкових умов на саму функцію у(х) та її похідні від першого до (n-1)-го порядку включно. В MathCAD можна вирішувати ЗДР вищих порядків, як з допомогою обчислювального блоку Given/Odesolve, так і шляхом зведення їх до системи рівнянь першого порядку.

У середині обчислювального блоку:

o ЗДР повинно бути лінійне відносно старшої похідної, тобто фактично повинне бути представлене в стандартній формі;

o початкові умови повинні мати вигляд у(х)=b або 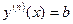, але не більш складний (наприклад ).

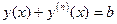В іншому, рішення ЗДР вищих порядків нічим не відрізняється від рішення рівнянь першого порядку.

7.5.Контрольні запитання.

1. Що називається звичайним диференціальне рівняння і диференціальним рівнянням в частинних похідних?

2. Що називається розв’язком диференціального рівняння ?

3. Як знайти частинний розв’язок диференціального рівняння?

4. Які задачі розрізняють в залежності від способу задання додаткових умов?

5. В чому полягає задача Коші?

6. Який має вигляд та як застосовується обчислювальний блок Given/Odesolve, що використовується для рішення одного ЗДР за допомогою методу Рунге-Кутта ?

7. Якими функціями можуть бути реалізовані чисельні рішення задачі Коші для диференціальних рівнянь і систем рівнянь?

8. Які особливості рішення ЗДР n-го порядку в MathCAD ?

Література

1. Інформатика. Комп’ютерна техніка. Комп’ютерні технології. Під ред.. проф. Пушкаря О.І. ─ К.: ВЦ „Академія”, 2003. ─ 704с.

2. Ляшенко М.Я., Головань М.С. Чисельні методи: Підручник. ─ К.: Либідь, 1996. ─ 288 с.

3. MathCAD 12. Для студентов и инженеров: Валерий Очков — Санкт-Петербург, БХВ-Петербург, 2005 г.- 464 с.

4. MathCAD 12: Е. Р. Алексеев, О. В. Чеснокова — Санкт-Петербург, НТ Пресс, 2005 г.- 352 с.

5. MathCAD 13 на примерах (+ CD-ROM): Алексей Васильев — Санкт-Петербург, БХВ-Петербург, 2006 г.- 528 с.

6. MathCAD 14 для студентов и инженеров. Русская версия: Валерий Очков — Москва, БХВ-Петербург, 2009 г.- 512 с.

7. MathCAD в инженерных расчетах (+ CD-ROM): Брент Максфилд — Санкт-Петербург, Корона-Век, МК-Пресс, 2010 г.- 368 с.

8. Вычисления в MATHCAD 12: Д. Гурский, Е. Турбина — Санкт-Петербург, Питер, 2006 г.- 544 с.

9. Самоучитель MathCAD 13: Дмитрий Кирьянов — Санкт-Петербург, БХВ-Петербург, 2006 г.- 528 с.

Зміст

Вступ. 3

Лекція 1. Основи роботи в системі MathCAD.. 4

1.1. Інтерфейс користувача. 4

1.2. Вхідна мова системи MathCAD. Типи даних. 9

1.3. Введення та редагування даних. 15

1.4. Налаштування MathCAD для роботи. 19

1.5. Контрольні запитання. 22

Лекція 2. Виконання обчислень над векторами та матрицями. 23

2.1 Виконання найпростіших обчислень над матрицями та векторами. 23

2.2. Векторні та матричні оператори. 25

2.3. Векторні та матричні функції. 27

2.4. Функції, що повертають спеціальні характеристики матриць. 29

2.5. Додаткові матричні функції. 30

2.6. Функції сортування для векторів і матриць. 31

2.7. Контрольні запитання. 31

Лекція 3. Графіка в системі MathCAD. 32

3.1. Засоби побудови графіків в системі MathCAD. 32

3.2. Графіки функцій однієї змінної в декартовій системі координат . 33

3.3. Двовимірні графіки в полярній системі координат. 34

3.4. Графіки в тривимірному просторі. 35

3.5. Анімація в MathCAD. 42

3.6. Контрольні запитання. 44

Лекція 4. Символьні обчислення в системі MathCAD. 45

4.1. Можливості символьного процесора MathCAD. 45

4.2. Команди меню Symbolics (Символьні операції). 46

4.3. Палітра символьних перетворень SmartMath. 49

4.4. Приклади: 49

4.5. Оптимізація. 51

4.6. Контрольні запитання. 51

Лекція 5. Програмування засобами MathCAD. 52

5.1.Створення програми. 52

5.2. Створення програмного модуля (Add line). 53

5.3. Розробка та редагування програми. 54

5.4. Локальне присвоєння (←). 55

5.5. Умовні оператори (if, otherwise). 56

5.6. Оператори циклу (for, while). 57

5.7. Оператори break, continue, return. 60

5.8. Виведення результатів розрахунків із програми. 61

5.9. Контрольні запитання. 62

Лекція 6. Рішення рівнянь та систем рівнянь. Пошук екстремумів функцій. 62

6.1. Рівняння з одним невідомим. 62

6.2. Корені полінома. 64

6.3. Системи рівнянь. 66

6.4. Пошук екстремумів функцій. 69

6.5. Контрольні запитання. 71

Лекція №7. Звичайні диференціальні рівняння. 72

7.1. ЗДР першого порядку. 72

7.2. Обчислювальний блок Given/Odesolve. 73

7.3. Вбудовані функції rкfixed, Rkadapt, Bulstoer. 74

7.4. ЗДР вищого порядку. 76

7.5.Контрольні запитання. 77

Література. 78

МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ